Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad   



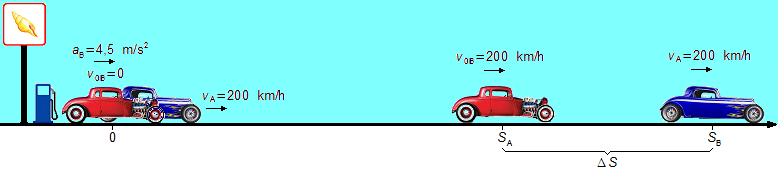
Un coche se desplaza por una carretera recta a una velocidad constante de 200 km/h. En el momento en que este coche pasa junto a otro coche, que inicialmente está parado en una gasolinera, este comienza a desplazarse con una aceleración constante de 4,5 m/s2 hasta alcanzar una velocidad de 200 km/h. Determine:
a) ¿Cuánto tiempo transcurre hasta que el coche que sale de la gasolinera alcanza una velocidad de 200 km/h?
b) ¿A qué distancia están los coches entre sí cuando sus velocidades son iguales?


Datos del problema:
  • Velocidad del carro A:    vA = 200 km/h;
  • Velocidad del carro B:    v0B = 0;
  • Velocidad final del carro B:    vB = 200 km/h;
  • Aceleración del carro B:    aB = 4,5 m/s2.
Esquema del problema:

Figura 1

Solución

Primero, vamos convertir las velocidades de los carros dadas de kilómetros por hora (km/h) a metros por segundo (m/s), que se utiliza en el Sistema Internacional de Unidades (SI)
\[ \begin{gather} v_{\small A}=v_{\small B}=200\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm h}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{200}{3,6}\;\frac{\mathrm m}{\mathrm s}=55,6\;\mathrm{m/s} \end{gather} \]
a) La ecuación horaria de la velocidad está dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {v=v_0+a t} \end{gather} \]
Para el carro B:
\[ \begin{gather} v_{\small B}=v_{0 B}+a_{\small B}t\\[5pt] 55,6=0+4,5t\\[5pt] t=\frac{55,6}{4,5} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t\approx 12,4\;\mathrm s} \end{gather} \]

b) El coche A se desplaza con velocidad constante, está en Movimiento Rectilíneo Uniforme (MRU), la ecuación horaria de este movimiento está dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+vt} \end{gather} \]
Aplicando esta ecuación, utilizando los datos del coche A y el intervalo de tiempo encontrado en el ítem (a)
\[ \begin{gather} S_{\small A}=S_{0\small A}+v_{\small A}t\\[5pt] S_{\small A}=0+55,6\times 12,4\\[5pt] S_{\small A}\approx 689,4\;\mathrm m \end{gather} \]
El coche B se desplaza con aceleración constante, está en Movimiento Rectilíneo Uniformemente Variado (MRUV), la ecuación horaria de este movimiento está dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{a}{2}t^2} \end{gather} \]
aplicando esta ecuación, utilizando los datos del coche B y el intervalo de tiempo encontrado en el ítem (a)
\[ \begin{gather} S_{\small B}=S_{0\small B}+v_{0\small B}t+\frac{a_{\small B}}{2}t^2\\[5pt] S_{\small B}=0+0t+\frac{4,5}{2}\times 12,4^2\\[5pt] S_{\small B}=346\;\mathrm m \end{gather} \]
La distancia entre los coches será dada por
\[ \begin{gather} \Delta S=|S_{\small A}-S_{\small B}|\\[5pt] \Delta S=|689,4-346| \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta S=343,4\;\mathrm m} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .