Solved Problem on One-dimensional Motion

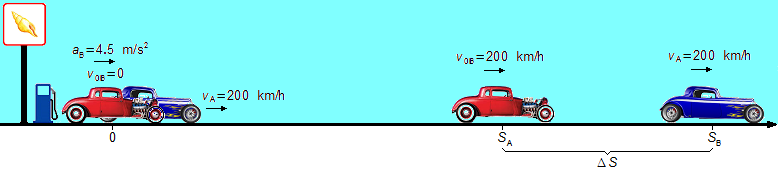
A car moves along a straight road with a speed of 200 km/h. When this car passes through another car, initially at rest at a gas station, it begins to move with a constant acceleration of 4.5 m/s² until it reaches the speed of 200 km/h. Determine:
a) What is the time elapsed until the car leaving the gas station reaches the speed of 200 km/h?
b) How far are they from each other when their speeds are equal?

Problem data:

Speed of car A: v_A = 200 km/h;
Initial speed of car B: v_0B = 0;
Final speed of car B: v_B = 200 km/h;
Acceleration of car B: a_B = 4.5 m/s².

Problem diagram:

Figure 1

Solution

First, let's convert the speeds of the cars given in kilometers per hour (km/h) to meters per second (m/s) used in the International System of Units (SI)

\[ \begin{gather} v_{\small A}=v_{\small B}=200\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm h}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{200}{3.6}\;\frac{\mathrm m}{\mathrm s}=55.6\;\mathrm{m/s} \end{gather} \]

a) The equation of velocity as a function of time is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {v=v_0+a t} \end{gather} \]

For car B:

\[ \begin{gather} v_{\small B}=v_{0 B}+a_{\small B}t\\[5pt] 55.6\;\mathrm{\small{\frac{m}{s}}}=0+\left(4.5\;\mathrm{\small{\frac{m}{s^2}}}\right)t\\[5pt] t=\frac{55.6\;\mathrm{\frac{\cancel m}{\cancel s}}}{4.5\;\mathrm{\frac{\cancel m}{s^\cancel 2}}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {t\approx 12.4\;\mathrm s} \end{gather} \]

b) The car A moves with constant speed, it is in Uniform Rectilinear Motion, the equation of displacement as a function of time is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+vt} \end{gather} \]

using this equation, the data from car A and the time interval found in item (a)

\[ \begin{gather} S_{\small A}=S_{0\small A}+v_{\small A}t\\[5pt] S_{\small A}=0+\left(55.6\;\mathrm{\small{\frac{m}{\cancel s}}}\right)\left(12.4\;\mathrm{\cancel s}\right)\\[5pt] S_{\small A}\approx 689.4\;\mathrm m \end{gather} \]

The car B moves with constant acceleration, it is in Uniformly Accelerated Rectilinear Motion, the equation of displacement as a function of this time is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{a}{2}t^2} \end{gather} \]

using this equation, the data from car B, and the time interval found in item (a)

\[ \begin{gather} S_{\small B}=S_{0\small B}+v_{0\small B}t+\frac{a_{\small B}}{2}t^2\\[5pt] S_{\small B}=0+0t+\;\left(\frac{4.5\;\mathrm{\frac{m}{s^2}}}{2}\right)(12.4\;\mathrm s)^2\\[5pt] S_{\small B}=346\;\mathrm m \end{gather} \]

The distance between the cars will be given by

\[ \begin{gather} \Delta S=|S_{\small A}-S_{\small B}|\\[5pt] \Delta S=|689.4\;\mathrm m-346\;\mathrm m| \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta S=343.4\;\mathrm m} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .