Exercice Résolu sur les Mouvement Unidimensionnel
publicité   



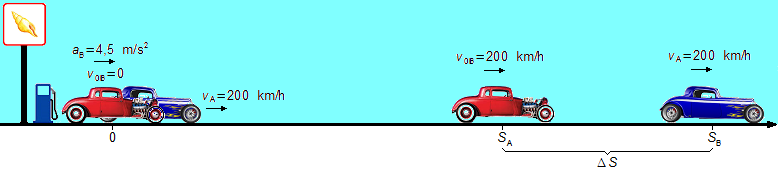
Un véhicule se déplace sur une route rectiligne à une vitesse constante de 200 km/h. Au moment où ce véhicule dépasse une autre voiture, initialement arrêtée à une station-service, celle-ci commence à se déplacer avec une accélération constante de 4,5 m/s2 jusqu'à atteindre la vitesse de 200 km/h. Déterminer:
a) Quel est l'intervalle de temps écoulé avant que la voiture qui quitte la station-service atteigne la vitesse de 200 km/h?
b) À quelle distance se trouve une voiture de l'autre lorsque leurs vitesses sont égales.


Données du problème:
  • Vitesse de la voiture A:    vA = 200 km/h;
  • Vitesse initiale de la voiture B:    v0B = 0;
  • Vitesse finale de la voiture B:    vB = 200 km/h;
  • Vitesse finale de la voiture B:    aB = 4,5 m/s2.
Schéma du problème:

Figure 1

Solution

Premièrement, nous allons convertir les vitesses des voitures données en kilomètres par heure (km/h) en mètres par seconde (m/s), utilisant le Système International d'Unités (SI)
\[ \begin{gather} v_{\small A}=v_{\small B}=200\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm h}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{200}{3,6}\;\frac{\mathrm m}{\mathrm s}=55,6\;\mathrm{m/s} \end{gather} \]
a) La équation horaire de la vitesse est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {v=v_0+a t} \end{gather} \]
Pour la voiture B:
\[ \begin{gather} v_{\small B}=v_{0 B}+a_{\small B}t\\[5pt] 55,6=0+4,5t\\[5pt] t=\frac{55,6}{4,5} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t\approx 12,4\;\mathrm s} \end{gather} \]

b) La voiture A se déplace à vitesse constante, elle est en Mouvement Rectiligne Uniforme, la équation horaire de ce mouvement est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+vt} \end{gather} \]
en appliquant cette équation, en utilisant les données de la voiture A et l'intervalle de temps trouvé dans l'article (a)
\[ \begin{gather} S_{\small A}=S_{0\small A}+v_{\small A}t\\[5pt] S_{\small A}=0+55,6\times 12,4\\[5pt] S_{\small A}\approx 689,4\;\mathrm m \end{gather} \]
La voiture B se déplace avec une accélération constante, elle est en Mouvement Rectiligne Uniformément Varié, la équation horaire de ce mouvement est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{a}{2}t^2} \end{gather} \]
en appliquant cette équation, en utilisant les données de la voiture B et l'intervalle de temps trouvé dans l'article (a)
\[ \begin{gather} S_{\small B}=S_{0\small B}+v_{0\small B}t+\frac{a_{\small B}}{2}t^2\\[5pt] S_{\small B}=0+0t+\frac{4,5}{2}\times 12,4^2\\[5pt] S_{\small B}=346\;\mathrm m \end{gather} \]
La distance entre les voitures sera donnée par
\[ \begin{gather} \Delta S=|S_{\small A}-S_{\small B}|\\[5pt] \Delta S=|689,4-346| \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta S=343,4\;\mathrm m} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .