Exercício Resolvido de Movimento Unidimensional
publicidade
Um trem-bala com velocidade constante de 234 km/h atravessa um túnel de 620 m de extensão, o comprimento do trem é de 160 m. Qual o intervalo de tempo para atravessar o túnel?
Dados do problema:
- Velocidade do trem: v = 234 km/h;
- Comprimento do trem: L = 160 m;
- Comprimento do túnel: LT = 620 m.
O trem possui dimensão relevante para o problema, ele é um objeto extenso.
Ele começa a atravessar o túnel quando a parte dianteira do trem chega na entrada do túnel e termina quando a parte traseira do trem chega na saída do túnel (Figura 1).
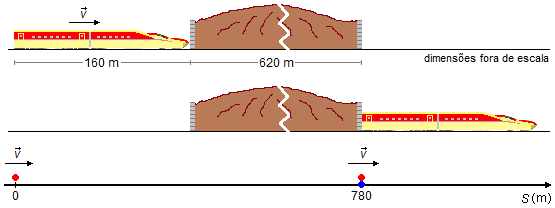
Tomando um sistema de referência orientado para a direita, o problema pode ser reduzido a um ponto material, que representa a parte traseira do trem na origem do referencial (S0=0) com velocidade v=234 km/h e um ponto dado pela soma dos comprimentos do trem e do túnel \( S=L+L_T=160+620=780\;\mathrm m \) que representa a saída do túnel.
Solução
Em primeiro lugar devemos converter a velocidade do trem dada em quilômetros por hora (km/h) para metros por segundo (m/s) usada no Sistema Internacional de Unidade (S.I.)
\[
\begin{gather}
v=234\;\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm{h}}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{234}{3,6}\;\frac{\mathrm m}{\mathrm s}=65\;\mathrm{m/s}
\end{gather}
\]
O intervalo de tempo será dado quando o ponto que representa a parte de trás do trem atingir o ponto que
representa a saída do túnel.O ponto está em Movimento Retilíneo Uniforme. (M.R.U.) dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt}
\end{gather}
\]
\[
\begin{gather}
780=0+65 t\\[5pt]
65 t=780\\[5pt]
t=\frac{780}{65}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=12\;\mathrm s}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .