A high-speed train with a constant speed of 234 km/h runs through a 620 m long tunnel, the length of the train is 160 m. What is the time interval to cross the tunnel?


Problem Data:

• Train speed:    v = 234 km/h;
• Train length:    L = 160 m;
• Tunnel length:    L_T = 620 m.

Problem diagram:

The train has a dimension essential to the problem, it is a large object.
It begins to cross the tunnel when the front of the train arrives at the tunnel entrance and ends when the rear of the train arrives at the tunnel exit (Figure 1).


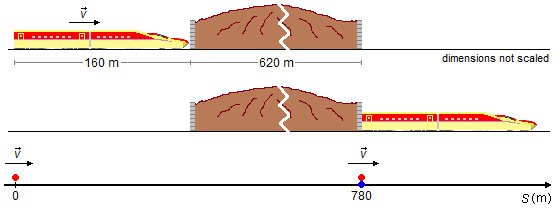
We choose a frame of reference oriented to the right. The problem can be reduced to a particle, which represents the rear of the train, at the origin of the frame (S₀=0), with speed v=234 km/h, and a point given by the sum of train and tunnel lengths \( S=L+L_T=160+620=780\;\mathrm m \) representing the tunnel exit.

Solution

First, we convert the speed of the train given in kilometers per hour (km/h) to meters per second (m/s) used in the International System of Units (SI) The time interval will be given when the point representing the back of the train reaches the point representing the tunnel exit.
The particle travels with constant speed, writing the equation of displacement as a function of time