Exercice Résolu sur les Mouvement Unidimensionnel
publicité
Un train à grande vitesse avec une vitesse constante de 234 km/h traverse un tunnel de 620 m de longueur, la longueur du train étant de 160 m. Quel est l'intervalle de temps pour traverser le tunnel?
Données du problème:
- Vitesse du train : v = 234 km/h;
- Longueur du train: L = 160 m;
- Longueur du tunnel: LT = 620 m.
Le train a une dimension importante pour le problème, c'est un objet étendu.
Il commence à traverser le tunnel lorsque l'avant du train atteint l'entrée du tunnel et se termine lorsque l'arrière du train atteint la sortie du tunnel (Figure 1).
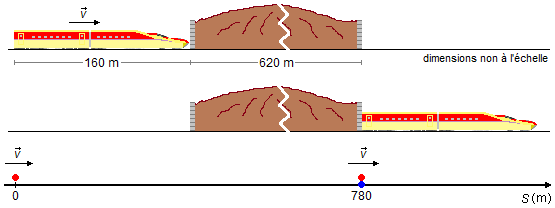
Nous choisissons un référentiel orienté vers la droite, le problème peut être réduit à un point matériel, représentant l'arrière du train à l'origine du référentiel (S0=0) avec une vitesse v = 234 km/h et un point donné par la somme des longueurs du train et du tunnel \( S=L+L_T=160+620=780\;\mathrm m \) , représentant la sortie du tunnel.
Solution
Premièrement, nous devons convertir la vitesse du train donnée en kilomètres par heure (km/h) en mètres par seconde (m/s) utilisée dans le Système International d'Unités (SI)
\[
\begin{gather}
v=234\;\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm{h}}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{234}{3,6}\;\frac{\mathrm m}{\mathrm s}=65\;\mathrm{m/s}
\end{gather}
\]
L'intervalle de temps sera donné lorsque le point représentant l'arrière du train atteindra le point
représentant la sortie du tunnel.Le point est en Mouvement Rectiligne Uniforme, donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt}
\end{gather}
\]
\[
\begin{gather}
780=0+65 t\\[5pt]
65 t=780\\[5pt]
t=\frac{780}{65}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=12\;\mathrm s}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .