Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
Un tren de alta velocidad con una velocidad constante de 234 km/h atraviesa un túnel de 620 m de longitud, y el tren tiene una longitud de 160 m. ¿Cuál es el intervalo de tiempo para atravesar el túnel?
Datos del problema:
- Velocidad del tren: v = 234 km/h;
- Longitud del tren: L = 160 m;
- Longitud del túnel: LT = 620 m.
El tren tiene dimensiones relevantes para el problema, es un objeto extenso.
Comienza a atravesar el túnel cuando la parte delantera del tren llega a la entrada del túnel y termina cuando la parte trasera del tren llega a la salida del túnel (Figura 1).
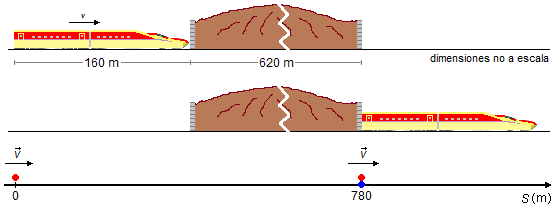
Tomando un sistema de referencia orientado hacia la derecha, el problema puede reducirse a un punto material, que representa la parte trasera del tren en el origen del referencial (S0=0) con velocidad v=234 km/h y un punto dado por la suma de las longitudes del tren y del túnel \( S=L+L_T=160+620=780\;\mathrm m \) que representa la salida del túnel.
Solución
En primer lugar, debemos convertir la velocidad del tren dada en kilómetros por hora (km/h) a metros por segundo (m/s) utilizada en el Sistema Internacional de Unidades (SI)
\[
\begin{gather}
v=234\;\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm{h}}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{234}{3,6}\;\frac{\mathrm m}{\mathrm s}=65\;\mathrm{m/s}
\end{gather}
\]
El intervalo de tiempo se dará cuando el punto que representa la parte trasera del tren alcance el punto que
representa la salida del túnel.El punto está en Movimiento Rectilíneo Uniforme (MRU) dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt}
\end{gather}
\]
\[
\begin{gather}
780=0+65 t\\[5pt]
65 t=780\\[5pt]
t=\frac{780}{65}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=12\;\mathrm s}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .