Ejercicio Resuelto sobre Dinámica
publicidad
Un bloque de 5 kg está bajo la acción de una fuerza variable en función del tiempo dada por
a) ¿Cuál es la aceleración del bloque en t = 2 s?
b) ¿Cuál es la velocidad del bloque en t = 5 s?
c) ¿Cuál es el desplazamiento del bloque entre t = 2 y t = 4 s?
\[
\begin{gather}
\qquad\qquad\qquad F_x=5t+2 \qquad\qquad\qquad \text{unidades (SI)}
\end{gather}
\]
sin otras fuerzas actuando en la dirección x. La velocidad inicial del bloque es igual a
0,5 m/s.a) ¿Cuál es la aceleración del bloque en t = 2 s?
b) ¿Cuál es la velocidad del bloque en t = 5 s?
c) ¿Cuál es el desplazamiento del bloque entre t = 2 y t = 4 s?
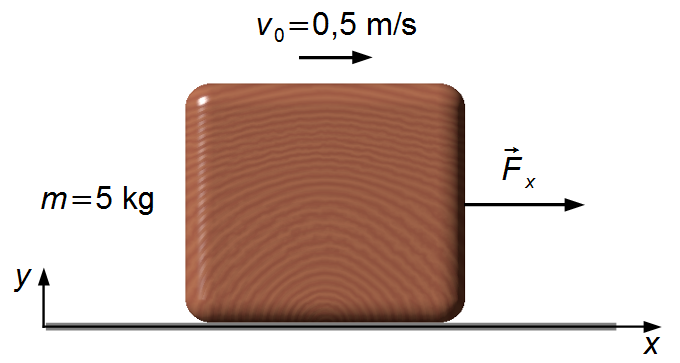
Datos del problema:
- Masa del bloque: m = 5 kg;
- Velocidad inicial del bloque: v0 = 0,5 m/s.
Tomamos un sistema de referencia con el eje-x orientado hacia la derecha y el eje-y hacia arriba (Figura 1).
Solución:
a) Aplicando la Segunda Ley de Newton en la dirección x, la fuerza dada en el problema es la única fuerza en esta dirección
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec F=m\vec a}
\end{gather}
\]
\[
\begin{gather}
F_x=ma_x\\[5pt]
5t+2=5a_x\\[5pt]
a_x=\frac{5t+2}{5} \tag{I}
\end{gather}
\]
para t = 2 s
\[
\begin{gather}
a_x=\frac{5\times2+2}{5}\\[5pt]
a_x=\frac{12}{5}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_x=2,4\;\mathrm{m/s}^2}
\end{gather}
\]
b) La aceleración está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a=\frac{dv}{dt}} \tag{II}
\end{gather}
\]
sustituyendo la fórmula (II) en la ecuación (I) del ítem anterior
\[
\begin{gather}
\frac{dv_x}{dt}=\frac{5t+2}{5}\\[5pt]
\frac{dv_{x}}{dt}=t+0,4
\end{gather}
\]
integrando en dt de ambos lados de la igualdad
\[
\begin{gather}
\int\frac{dv_x}{dt}\;dt=\int t+0,4\;dt\\[5pt]
\int dv_x=\int t+0,4\;dt
\end{gather}
\]
en el lado derecho de la igualdad, la integral de la suma es igual a la suma de las integrales, y el factor
constante 0,4 sale de la integral
\[
\begin{gather}
\int dv_x=\int t\;dt+0,4\int dt
\end{gather}
\]
Integral de \( \displaystyle \int dv_x \)
\[
\begin{gather}
\int 1\;dv_x=v_x+C_1
\end{gather}
\]
Integral de \( \displaystyle \int t\;dt \)
\[
\begin{gather}
\int t\;dt=\frac{t^{1+1}}{1+1}+C_1=\frac{t^2}{2}+C_1
\end{gather}
\]
Integral de \( \displaystyle \int dt \)
\[
\begin{gather}
\int 1\;dt=t+C_3
\end{gather}
\]
donde C1, C2 y C3 son constantes de integración
\[
\begin{gather}
v_x+C_{1}=\frac{t^2}{2}+C_1+0,4t+C_3\\[5pt]
v_x=\frac{t^2}{2}+0,4t+C_{3}+C_1-C_1
\end{gather}
\]
definiendo las constantes C1, C2 y C3 como una nueva
constante C
\[
\begin{gather}
C\equiv C_3+C_1-C_1
\end{gather}
\]
La ecuación de la velocidad es de la forma
\[
\begin{gather}
v_x=\frac{t^2}{2}+0,4t+C
\end{gather}
\]
La constante C se determina usando la condición inicial dada en el problema, en t = 0,
vx = 0,5 m/s
\[
\begin{gather}
v_x=\frac{t^{2}}{2}+0,4t+C\\[5pt]
0,5=\frac{0^2}{2}+0,4\times 0+C\\[5pt]
C=0,5\;\mathrm{m/s}
\end{gather}
\]
La ecuación de la velocidad será
\[
\begin{gather}
v_x=\frac{t^2}{2}+0,4t+0,5 \tag{III}
\end{gather}
\]
para t = 5 s
\[
\begin{gather}
v_x=\frac{5^2}{2}+0,4\times 5+0,5\\[5pt]
v_x=\frac{25}{2}+2+0,5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_x=15\;\mathrm{m/s}}
\end{gather}
\]
c) La velocidad está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\frac{dx}{dt}} \tag{IV}
\end{gather}
\]
sustituyendo la fórmula (IV) en la ecuación (III) del ítem anterior
\[
\begin{gather}
\frac{dx}{dt}=\frac{t^2}{2}+0,4t+0,5
\end{gather}
\]
integrando en dt de ambos lados de la igualdad
\[
\begin{gather}
\int\frac{dx}{dt}\;dt=\int\frac{t^2}{2}+0,4t+0,5\;dt\\[5pt]
\int dx=\int \frac{t^2}{2}+0,4t+0,5\;dt
\end{gather}
\]
en el lado derecho de la igualdad, la integral de la suma es igual a la suma de las integrales, y los
factores constantes
\( \frac{1}{2} \)
0,4 y 0,5 salen de la integral
\[
\begin{gather}
\int dx=\frac{1}{2}\int t^2\;dt+0,4\int t\;dt+0,5\int dt
\end{gather}
\]
Integral de \( \displaystyle \int dx \)
\[
\begin{gather}
\int 1\;dx=x+C_4
\end{gather}
\]
Integral de \( \displaystyle \int t^2\;dt \)
\[
\begin{gather}
\int t^2\;dt=\frac{t^{2+1}}{2+1}+C_5=\frac{t^{3}}{3}+C_5
\end{gather}
\]
donde C4 y C5 son constantes de integración. Las dos últimas integrales del lado derecho de la igualdad ya se han calculado anteriormente
\[
\begin{gather}
x+C_4=\frac{1}{2}\times{\frac{t^{3}}{3}}+C_5+0,4\frac{t^2}{2}+C_6+0,5t+C_7\\[5pt]
x=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t+C_5+C_6+C_7-C_4
\end{gather}
\]
definiendo las constantes C4, C5, C6 y
C7 como una nueva constante C'
\[
\begin{gather}
C'\equiv C_5+C_6+C_7-C_4
\end{gather}
\]
La ecuación de la posición es de la forma
\[
\begin{gather}
x=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t+C'
\end{gather}
\]
El problema no proporciona la posición inicial del bloque, pero podemos determinar la constante C'
asumiendo que en t = 0, x = 0
\[
\begin{gather}
0=\frac{0^{3}}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'\\[5pt]
C'=0
\end{gather}
\]
La ecuación de la posición será
\[
\begin{gather}
x=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t
\end{gather}
\]
para t = 2 s
\[
\begin{gather}
x_1=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2\\[5pt]
x_1=\frac{4}{3}+0,8+1\\[5pt]
x_1=3,1\;\mathrm m
\end{gather}
\]
para t = 4 s
\[
\begin{gather}
x_4=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4\\[5pt]
x_4=\frac{343}{6}+0,2\times49+3,5\\[5pt]
x_4=15,9\;\mathrm m
\end{gather}
\]
El desplazamiento entre los instantes de 2 s y 4 s será
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\Delta x=x_f-x_i}
\end{gather}
\]
\[
\begin{gather}
\Delta x=x_4-x_1\\[5pt]
\Delta x=15,9-3,1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta x=12,8\;\mathrm m}
\end{gather}
\]
Observación: ¿Qué nos permite hacer la suposición de que en t = 0 tenemos
x = 0?
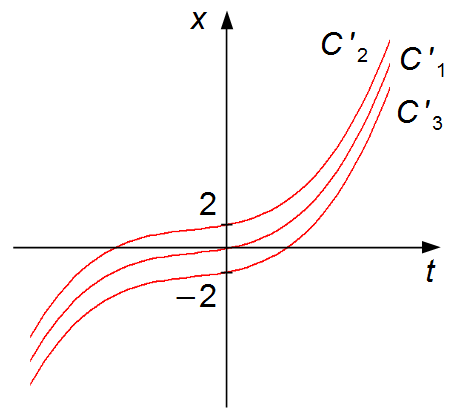 Gráfico 1
Gráfico 1
El eje de las abscisas representa el tiempo t, como no existe tiempo negativo, construiremos el gráfico para valores del semieje real positivo t.
Determinación de C' para diferentes valores de x y t:
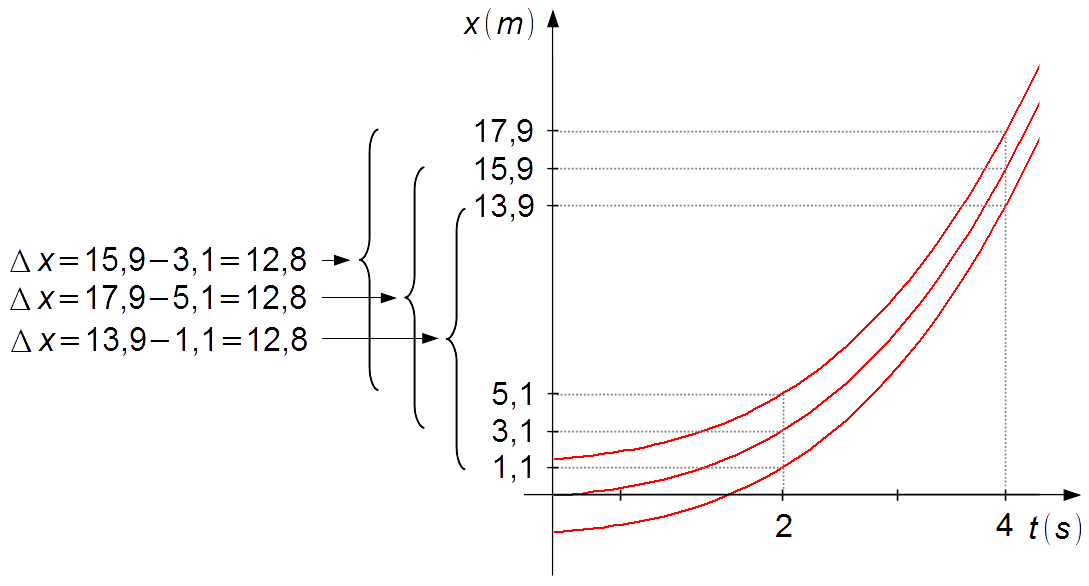 Gráfico 2
Gráfico 2
Calculando el valor de x(t) para t = 2 s y t = 4 s, usando varios valores de C' = 0, 2, −2 (Gráfico 2).
Para otros dos instantes cualquiera elegidos (por ejemplo, 1 s y 7 s, o 12 s y 23 s, o 35 s y 100 s, etc.), los desplazamientos serán diferentes de 12,8 m, porque el bloque está acelerado por la fuerza aplicada. Pero los desplazamientos serán iguales entre esos instantes para las mismas posiciones iniciales elegidas.
En este problema, la posición está dada por una función de tercer grado
\[
\begin{gather}
x(t)=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t+C'
\end{gather}
\]
el término C', independiente del tiempo t, solo desplaza el gráfico de la función a lo
largo del eje-x (eje de las ordenadas, hacia arriba o hacia abajo). Cuanto mayor sea el valor
de C', el gráfico se desplaza hacia la dirección de x positivo (hacia arriba). Cuanto
menor sea el valor de C', el gráfico se desplaza hacia la dirección de x negativo
(hacia abajo) (Gráfico 1).

El eje de las abscisas representa el tiempo t, como no existe tiempo negativo, construiremos el gráfico para valores del semieje real positivo t.
Determinación de C' para diferentes valores de x y t:
-
Para t = 0 y x = 0
\( \displaystyle x(0)=0=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_1\Rightarrow C'_1=0 \)\[ x(0)=0=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_1\Rightarrow C'_1=0 \]; -
Para t = 0 y x = 2
\( \displaystyle x(0)=2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times0+C'_1\Rightarrow C'_1=2 \)\[ \displaystyle x(0)=2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times0+C'_1\Rightarrow C'_1=2 \]; -
Para t = 0 y x = −2
\( \displaystyle x(0)=-2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_3\Rightarrow C'_3=-2 \)\[ \displaystyle x(0)=-2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_3\Rightarrow C'_3=-2 \];

Calculando el valor de x(t) para t = 2 s y t = 4 s, usando varios valores de C' = 0, 2, −2 (Gráfico 2).
-
Para C' = 0
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2=3,1\;\mathrm{m} \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2=3,1\;\mathrm{m} \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4=15,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4=15,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=15,9-3,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=15,9-3,1=12,8\;\mathrm m \]
-
Para C' = 2
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times {\frac{2^2}{2}}+0,5\times 2+2=5,1\;\mathrm m \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times {\frac{2^2}{2}}+0,5\times 2+2=5,1\;\mathrm m \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+4\times 4+2=17,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+4\times 4+2=17,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=17,9-5,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=17,9-5,1=12,8\;\mathrm m \]
-
Para C' = −2
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2-2=1,1\;\mathrm m \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2-2=1,1\;\mathrm m \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4-2=13,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4-2=13,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=13,9-1,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=13,9-1,1=12,8\;\mathrm m \]
Para otros dos instantes cualquiera elegidos (por ejemplo, 1 s y 7 s, o 12 s y 23 s, o 35 s y 100 s, etc.), los desplazamientos serán diferentes de 12,8 m, porque el bloque está acelerado por la fuerza aplicada. Pero los desplazamientos serán iguales entre esos instantes para las mismas posiciones iniciales elegidas.
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .