Exercice Résolu sur les Dynamique
EN
ES
PT-BR
publicité
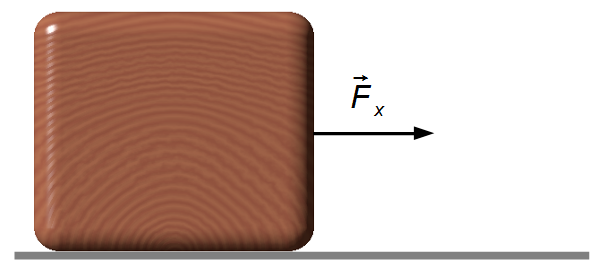
Un bloc de 5 kg est soumis à l'action d'une force variable en fonction du temps donnée par
a) Quelle est l'accélération du bloc à t = 2 s?
b) Quelle est la vitesse du bloc à t = 5 s?
c) Quel est le déplacement du bloc entre t = 2 s et t = 4 s?
\[
\begin{gather}
\qquad\qquad\qquad F_x=5t+2 \qquad\qquad\qquad \text{unités (SI)}
\end{gather}
\]
sans aucune autre force agissant dans la direction x. La vitesse initiale du bloc est de
0,5 m/s.a) Quelle est l'accélération du bloc à t = 2 s?
b) Quelle est la vitesse du bloc à t = 5 s?
c) Quel est le déplacement du bloc entre t = 2 s et t = 4 s?
Données du problème:
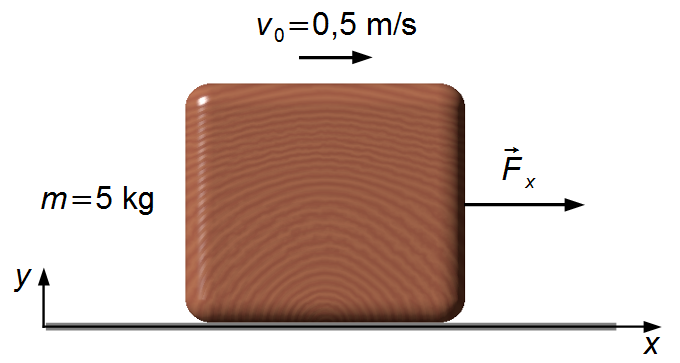
- Masse du bloc: m = 5 kg;
- Vitesse initiale du bloc: v0 = 0,5 m/s.
Nous choisissons un référentiel avec l'axe-x orienté vers la droite et l'axe-y vers le haut (Figure 1).
Solution:
a) En appliquant la Deuxième Loi de Newton dans la direction x, la force donnée dans le problème est la seule force dans cette direction
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec F=m\vec a}
\end{gather}
\]
\[
\begin{gather}
F_x=ma_x\\[5pt]
5t+2=5a_x\\[5pt]
a_x=\frac{5t+2}{5} \tag{I}
\end{gather}
\]
pour t = 2 s
\[
\begin{gather}
a_x=\frac{5\times2+2}{5}\\[5pt]
a_x=\frac{12}{5}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_x=2,4\;\mathrm{m/s}^2}
\end{gather}
\]
b) L'accélération est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a=\frac{dv}{dt}} \tag{II}
\end{gather}
\]
en substituant la formule (II) dans l'équation (I) de la partie précédente
\[
\begin{gather}
\frac{dv_x}{dt}=\frac{5t+2}{5}\\[5pt]
\frac{dv_{x}}{dt}=t+0,4
\end{gather}
\]
en intégrant par rapport à dt des deux côtés de l'égalité
\[
\begin{gather}
\int\frac{dv_x}{dt}\;dt=\int t+0,4\;dt\\[5pt]
\int dv_x=\int t+0,4\;dt
\end{gather}
\]
du côté droit de l'égalité, l'intégrale de la somme est égale à la somme des intégrales, et le facteur
constant 0,4 sort de l'intégrale
\[
\begin{gather}
\int dv_x=\int t\;dt+0,4\int dt
\end{gather}
\]
Intégrale de \( \displaystyle \int dv_x \)
\[
\begin{gather}
\int 1\;dv_x=v_x+C_1
\end{gather}
\]
Intégrale de \( \displaystyle \int t\;dt \)
\[
\begin{gather}
\int t\;dt=\frac{t^{1+1}}{1+1}+C_1=\frac{t^2}{2}+C_1
\end{gather}
\]
Intégrale de \( \displaystyle \int dt \)
\[
\begin{gather}
\int 1\;dt=t+C_3
\end{gather}
\]
où C1, C2 et C3 sont des constantes d'intégration
\[
\begin{gather}
v_x+C_{1}=\frac{t^2}{2}+C_1+0,4t+C_3\\[5pt]
v_x=\frac{t^2}{2}+0,4t+C_{3}+C_1-C_1
\end{gather}
\]
en définissant les constantes C1, C2 et C3 comme une
nouvelle constante C
\[
\begin{gather}
C\equiv C_3+C_1-C_1
\end{gather}
\]
L'équation de la vitesse est de la forme
\[
\begin{gather}
v_x=\frac{t^2}{2}+0,4t+C
\end{gather}
\]
La constante C est déterminée en utilisant la condition initiale donnée dans le problème, à
t = 0, vx = 0,5 m/s
\[
\begin{gather}
v_x=\frac{t^{2}}{2}+0,4t+C\\[5pt]
0,5=\frac{0^2}{2}+0,4\times 0+C\\[5pt]
C=0,5\;\mathrm{m/s}
\end{gather}
\]
L'équation de la vitesse sera
\[
\begin{gather}
v_x=\frac{t^2}{2}+0,4t+0,5 \tag{III}
\end{gather}
\]
pour t = 5 s
\[
\begin{gather}
v_x=\frac{5^2}{2}+0,4\times 5+0,5\\[5pt]
v_x=\frac{25}{2}+2+0,5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_x=15\;\mathrm{m/s}}
\end{gather}
\]
c) La vitesse est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\frac{dx}{dt}} \tag{IV}
\end{gather}
\]
en substituant la formule (IV) dans l'équation (III) de la partie précédente
\[
\begin{gather}
\frac{dx}{dt}=\frac{t^2}{2}+0,4t+0,5
\end{gather}
\]
en intégrant par rapport à dt des deux côtés de l'égalité
\[
\begin{gather}
\int\frac{dx}{dt}\;dt=\int\frac{t^2}{2}+0,4t+0,5\;dt\\[5pt]
\int dx=\int \frac{t^2}{2}+0,4t+0,5\;dt
\end{gather}
\]
du côté droit de l'égalité, l'intégrale de la somme est égale à la somme des intégrales, et les facteurs
constants
\( \frac{1}{2} \)
0,4 et 0,5 sortent de l'intégrale
\[
\begin{gather}
\int dx=\frac{1}{2}\int t^2\;dt+0,4\int t\;dt+0,5\int dt
\end{gather}
\]
Intégrale de \( \displaystyle \int dx \)
\[
\begin{gather}
\int 1\;dx=x+C_4
\end{gather}
\]
Intégrale de \( \displaystyle \int t^2\;dt \)
\[
\begin{gather}
\int t^2\;dt=\frac{t^{2+1}}{2+1}+C_5=\frac{t^{3}}{3}+C_5
\end{gather}
\]
où C4 et C5 sont des constantes d'intégration. Les deux dernières intégrales du côté droit de l'égalité ont déjà été calculées ci-dessus
\[
\begin{gather}
x+C_4=\frac{1}{2}\times{\frac{t^{3}}{3}}+C_5+0,4\frac{t^2}{2}+C_6+0,5t+C_7\\[5pt]
x=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t+C_5+C_6+C_7-C_4
\end{gather}
\]
en définissant les constantes C4, C5, C6 et
C7 comme une nouvelle constante C'
\[
\begin{gather}
C'\equiv C_5+C_6+C_7-C_4
\end{gather}
\]
L'équation de la position est de la forme
\[
\begin{gather}
x=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t+C'
\end{gather}
\]
Le problème ne fournit pas la position initiale du bloc, mais nous pouvons déterminer la constante C'
en supposant qu'à t = 0, x = 0
\[
\begin{gather}
0=\frac{0^{3}}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'\\[5pt]
C'=0
\end{gather}
\]
L'équation de la position sera
\[
\begin{gather}
x=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t
\end{gather}
\]
pour t = 2 s
\[
\begin{gather}
x_1=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2\\[5pt]
x_1=\frac{4}{3}+0,8+1\\[5pt]
x_1=3,1\;\mathrm m
\end{gather}
\]
pour t = 4 s
\[
\begin{gather}
x_4=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4\\[5pt]
x_4=\frac{343}{6}+0,2\times49+3,5\\[5pt]
x_4=15,9\;\mathrm m
\end{gather}
\]
Le déplacement entre les instants 2 s et 4 s sera
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\Delta x=x_f-x_i}
\end{gather}
\]
\[
\begin{gather}
\Delta x=x_4-x_1\\[5pt]
\Delta x=15,9-3,1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta x=12,8\;\mathrm m}
\end{gather}
\]
Remarque: Qu'est-ce qui nous permet de supposer qu'à t = 0, nous avons x = 0?
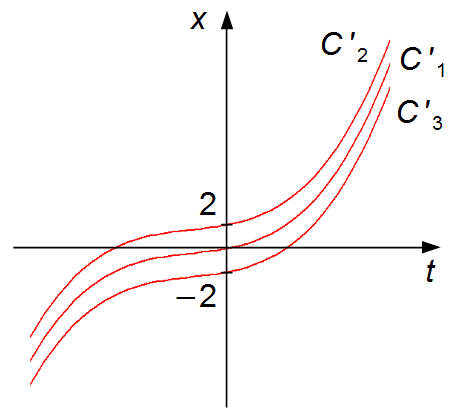Graphique 1
L'axe des abscisses représente le temps t. Comme il n'existe pas de temps négatif, nous allons construire le graphique pour les valeurs du demi-axe réel positif t.
Détermination de C' pour différentes valeurs de x et t:
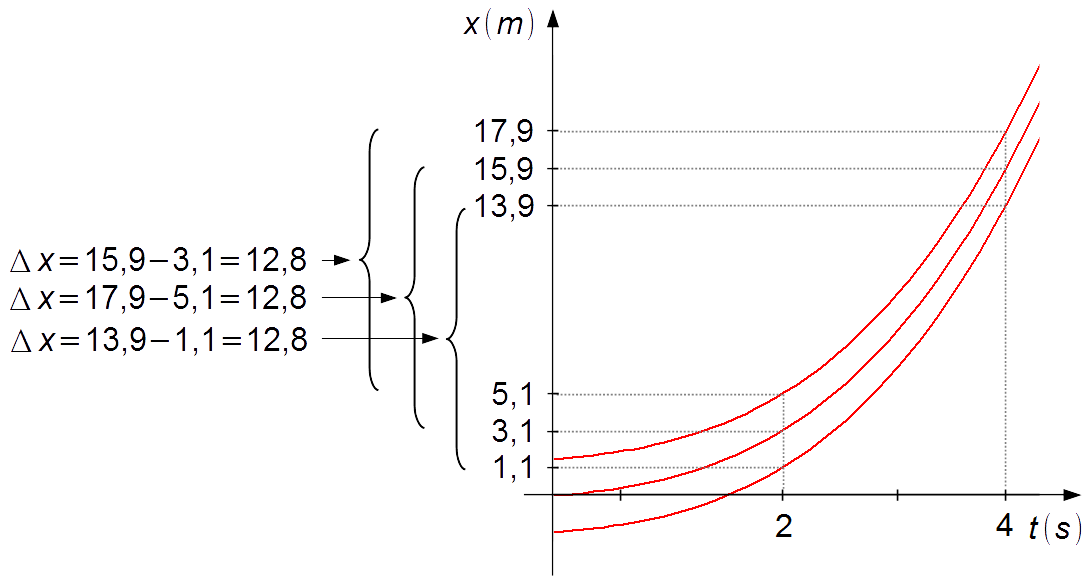Graphique 2
Calcul du déplacement x(t) pour t = 2 s et t = 4 s, en utilisant plusieurs valeurs de C' = 0, 2, −2 (Graphique 2).
Pour deux autres instants choisis (par exemple, 1 s et 7 s, ou 12 s et 23 s, ou 35 s et 100 s, etc.), les déplacements seront différents de 12,8 m, car le bloc est accéléré par la force appliquée. Mais les déplacements seront égaux entre ces instants pour les mêmes positions initiales choisies.
Dans ce problème, la position est donnée par une fonction cubique
\[
\begin{gather}
x(t)=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t+C'
\end{gather}
\]
le terme C', indépendant du temps t, déplace simplement le graphique de la fonction le
long de l'axe-x (axe des ordonnées – vers le haut ou vers le bas). Plus la valeur de C'
est grande, plus le graphique se déplace vers x positif (vers le haut). Plus la valeur de
C' est petite, plus le graphique se déplace vers x négatif (vers le bas) (Graphique 1).
L'axe des abscisses représente le temps t. Comme il n'existe pas de temps négatif, nous allons construire le graphique pour les valeurs du demi-axe réel positif t.
Détermination de C' pour différentes valeurs de x et t:
-
Pour t = 0 et x = 0
\( \displaystyle x(0)=0=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_1\Rightarrow C'_1=0 \)\[ x(0)=0=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_1\Rightarrow C'_1=0 \]; -
Pour t = 0 et x = 2
\( \displaystyle x(0)=2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times0+C'_1\Rightarrow C'_1=2 \)\[ \displaystyle x(0)=2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times0+C'_1\Rightarrow C'_1=2 \]; -
Pour t = 0 et x = −2
\( \displaystyle x(0)=-2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_3\Rightarrow C'_3=-2 \)\[ \displaystyle x(0)=-2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_3\Rightarrow C'_3=-2 \];
Calcul du déplacement x(t) pour t = 2 s et t = 4 s, en utilisant plusieurs valeurs de C' = 0, 2, −2 (Graphique 2).
-
Pour C' = 0
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2=3,1\;\mathrm{m} \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2=3,1\;\mathrm{m} \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4=15,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4=15,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=15,9-3,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=15,9-3,1=12,8\;\mathrm m \]
-
Pour C' = 2
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times {\frac{2^2}{2}}+0,5\times 2+2=5,1\;\mathrm m \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times {\frac{2^2}{2}}+0,5\times 2+2=5,1\;\mathrm m \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+4\times 4+2=17,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+4\times 4+2=17,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=17,9-5,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=17,9-5,1=12,8\;\mathrm m \]
-
Pour C' = −2
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2-2=1,1\;\mathrm m \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2-2=1,1\;\mathrm m \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4-2=13,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4-2=13,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=13,9-1,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=13,9-1,1=12,8\;\mathrm m \]
Pour deux autres instants choisis (par exemple, 1 s et 7 s, ou 12 s et 23 s, ou 35 s et 100 s, etc.), les déplacements seront différents de 12,8 m, car le bloc est accéléré par la force appliquée. Mais les déplacements seront égaux entre ces instants pour les mêmes positions initiales choisies.
publicité
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .