Solved Problem on Dynamics
advertisement
A 5 kg block is under the action of a force that varies with time, given by
a) What is the acceleration of the block at t = 2 s?
b) What is the velocity of the block at t = 5 s?
c) What is the displacement of the block between t = 2 s and t = 4 s?
\[
\begin{gather}
\qquad\qquad\qquad F_x=5t+2 \qquad\qquad\qquad \text{units (SI)}
\end{gather}
\]
with no other forces acting in the x-direction. The initial velocity of the block is 0.5 m/s.a) What is the acceleration of the block at t = 2 s?
b) What is the velocity of the block at t = 5 s?
c) What is the displacement of the block between t = 2 s and t = 4 s?
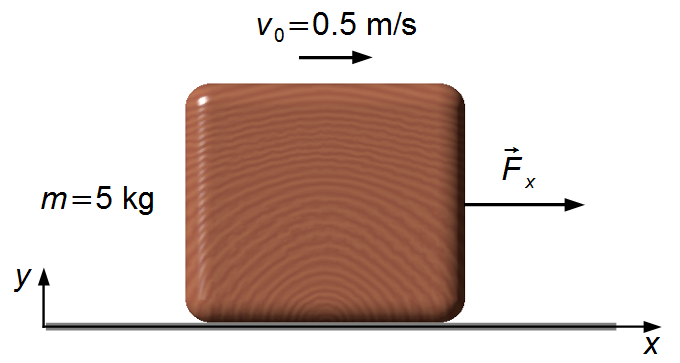
Problem data:
- Mass of the block: m = 5 kg;
- Initial velocity of the block: v0 = 0.5 m/s.
We choose a reference frame with the x-axis oriented to the right and the y-axis upward (Figure 1).
Solution:
a) Applying Newton's Second Law in the x-direction, the force given in the problem is the only force in this direction
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec F=m\vec a}
\end{gather}
\]
\[
\begin{gather}
F_x=ma_x\\[5pt]
5t+2=5a_x\\[5pt]
a_x=\frac{5t+2}{5} \tag{I}
\end{gather}
\]
for t = 2 s
\[
\begin{gather}
a_x=\frac{5\times2+2}{5}\\[5pt]
a_x=\frac{12}{5}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_x=2.4\;\mathrm{m/s}^2}
\end{gather}
\]
b) The acceleration is giben by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a=\frac{dv}{dt}} \tag{II}
\end{gather}
\]
substituting formula (II) into equation (I) from the previous item
\[
\begin{gather}
\frac{dv_x}{dt}=\frac{5t+2}{5}\\[5pt]
\frac{dv_{x}}{dt}=t+0.4
\end{gather}
\]
integrating with respect to dt on both sides of the equation
\[
\begin{gather}
\int\frac{dv_x}{dt}\;dt=\int t+0.4\;dt\\[5pt]
\int dv_x=\int t+0.4\;dt
\end{gather}
\]
on the right-hand side, the integral of the sum equals the sum of the integrals, and the constant factor
0.4 is factored out of the integral
\[
\begin{gather}
\int dv_x=\int t\;dt+0.4\int dt
\end{gather}
\]
Integral of \( \displaystyle \int dv_x \)
\[
\begin{gather}
\int 1\;dv_x=v_x+C_1
\end{gather}
\]
Integral of \( \displaystyle \int t\;dt \)
\[
\begin{gather}
\int t\;dt=\frac{t^{1+1}}{1+1}+C_1=\frac{t^2}{2}+C_1
\end{gather}
\]
Integral of \( \displaystyle \int dt \)
\[
\begin{gather}
\int 1\;dt=t+C_3
\end{gather}
\]
where C1, C2 and C3 are constants of integration
\[
\begin{gather}
v_x+C_{1}=\frac{t^2}{2}+C_1+0.4t+C_3\\[5pt]
v_x=\frac{t^2}{2}+0.4t+C_{3}+C_1-C_1
\end{gather}
\]
defining constants C1, C2 and C3 as a new constant
C
\[
\begin{gather}
C\equiv C_3+C_1-C_1
\end{gather}
\]
The velocity equation is of the form
\[
\begin{gather}
v_x=\frac{t^2}{2}+0.4t+C
\end{gather}
\]
The constant C is determined using the initial condition given in the problem: at t = 0,
vx = 0.5 m/s
\[
\begin{gather}
v_x=\frac{t^{2}}{2}+0.4t+C\\[5pt]
0.5=\frac{0^2}{2}+0.4\times 0+C\\[5pt]
C=0.5\;\mathrm{m/s}
\end{gather}
\]
The velocity equation will be
\[
\begin{gather}
v_x=\frac{t^2}{2}+0.4t+0.5 \tag{III}
\end{gather}
\]
for t = 5 s
\[
\begin{gather}
v_x=\frac{5^2}{2}+0.4\times 5+0.5\\[5pt]
v_x=\frac{25}{2}+2+0.5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_x=15\;\mathrm{m/s}}
\end{gather}
\]
c) The velocity is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\frac{dx}{dt}} \tag{IV}
\end{gather}
\]
substituting formula (IV) into equation (III) from the previous item
\[
\begin{gather}
\frac{dx}{dt}=\frac{t^2}{2}+0.4t+0.5
\end{gather}
\]
integrating with respect to dt on both sides of the equation
\[
\begin{gather}
\int\frac{dx}{dt}\;dt=\int\frac{t^2}{2}+0.4t+0.5\;dt\\[5pt]
\int dx=\int \frac{t^2}{2}+0.4t+0.5\;dt
\end{gather}
\]
on the right-hand side, the integral of the sum equals the sum of the integrals, and the constant factors
\( \frac{1}{2} \)
0.4 and 0.5 are factored out of the integral
\[
\begin{gather}
\int dx=\frac{1}{2}\int t^2\;dt+0.4\int t\;dt+0.5\int dt
\end{gather}
\]
Integral of \( \displaystyle \int dx \)
\[
\begin{gather}
\int 1\;dx=x+C_4
\end{gather}
\]
Integral of \( \displaystyle \int t^2\;dt \)
\[
\begin{gather}
\int t^2\;dt=\frac{t^{2+1}}{2+1}+C_5=\frac{t^{3}}{3}+C_5
\end{gather}
\]
where C4 and C5 are constants of integration. The last two integrals on the right-hand side have already been calculated above
\[
\begin{gather}
x+C_4=\frac{1}{2}\times{\frac{t^{3}}{3}}+C_5+0.4\frac{t^2}{2}+C_6+0.5t+C_7\\[5pt]
x=\frac{t^3}{6}+0.4\frac{t^2}{2}+0.5t+C_5+C_6+C_7-C_4
\end{gather}
\]
defining constants C4, C5, C6 and
C7 as a new constant C'
\[
\begin{gather}
C'\equiv C_5+C_6+C_7-C_4
\end{gather}
\]
The position equation is of the form
\[
\begin{gather}
x=\frac{t^3}{6}+0.4\frac{t^2}{2}+0.5t+C'
\end{gather}
\]
The problem does not provide the initial position of the block, but we can determine constant C' by
assuming that at t = 0, x = 0
\[
\begin{gather}
0=\frac{0^{3}}{6}+0.4\times{\frac{0^2}{2}}+0.5\times 0+C'\\[5pt]
C'=0
\end{gather}
\]
The position equation will be
\[
\begin{gather}
x=\frac{t^3}{6}+0.4\frac{t^2}{2}+0.5t
\end{gather}
\]
for t = 2 s
\[
\begin{gather}
x_1=\frac{2^3}{6}+0.4\times{\frac{2^2}{2}}+0.5\times2\\[5pt]
x_1=\frac{4}{3}+0.8+1\\[5pt]
x_1=3.1\;\mathrm m
\end{gather}
\]
for t = 4 s
\[
\begin{gather}
x_4=\frac{4^3}{6}+0.4\times{\frac{4^2}{2}}+0.5\times 4\\[5pt]
x_4=\frac{343}{6}+0.2\times49+3.5\\[5pt]
x_4=15.9\;\mathrm m
\end{gather}
\]
The displacement between times 2 s and 4 s will be
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\Delta x=x_f-x_i}
\end{gather}
\]
\[
\begin{gather}
\Delta x=x_4-x_1\\[5pt]
\Delta x=15.9-3.1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta x=12.8\;\mathrm m}
\end{gather}
\]
Note: What allows us to assume that at t = 0, we have x = 0?
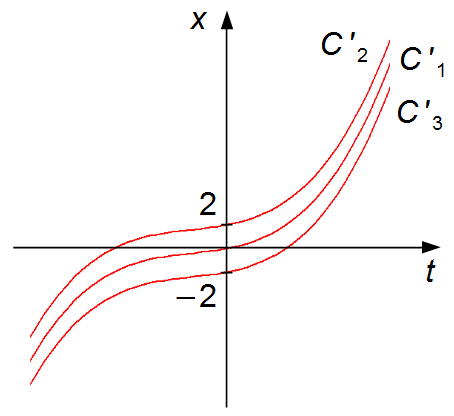 Graph 1
Graph 1
The horizontal axis represents time t. Since negative time doesn't exist, we'll construct the graph for values of the positive real semi-axis t.
Determination of C' for different values of x and t:
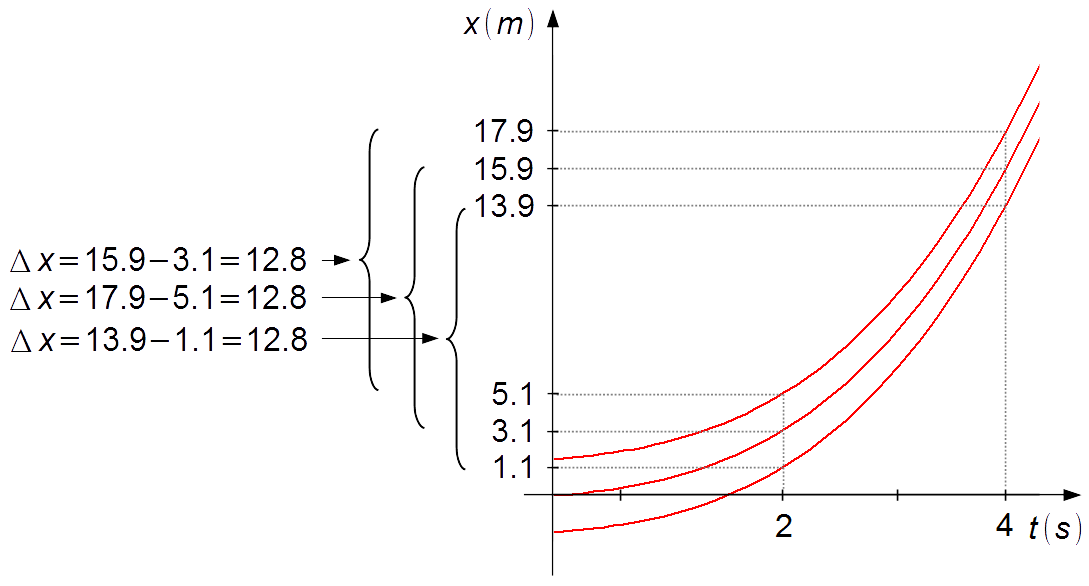 Graph 2
Graph 2
Calculating the value of x(t) for t = 2 s and t = 4 s, using various values ofC' = 0, 2, −2 (Graph 2).
For any other chosen instants (for example, 1 s and 7 s, or 12 s and 23 s, or 35 s and 100 s, etc.), the displacements will differ from 12.8 m, because the block is accelerated by the applied force. However, the displacements between those times will be the same for the same initial positions chosen.
In this problem, the position is given by a cubic function
\[
\begin{gather}
x(t)=\frac{t^3}{6}+0.4\frac{t^2}{2}+0.5t+C'
\end{gather}
\]
the term C', independent of time t, only shifts the graph of the function along the
x-axis (the vertical axis - up and down). The larger the value of C', the more the
graph shifts in the positive x-direction (upward). The smaller the value of C', the
more the graph shifts in the negative x-direction (downward) (Graph 1).

The horizontal axis represents time t. Since negative time doesn't exist, we'll construct the graph for values of the positive real semi-axis t.
Determination of C' for different values of x and t:
-
For t = 0 and x = 0
\( \displaystyle x(0)=0=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_1\Rightarrow C'_1=0 \)\[ x(0)=0=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_1\Rightarrow C'_1=0 \]; -
For t = and e x = 2
\( \displaystyle x(0)=2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times0+C'_1\Rightarrow C'_1=2 \)\[ \displaystyle x(0)=2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times0+C'_1\Rightarrow C'_1=2 \]; -
For t = 0 and x = −2
\( \displaystyle x(0)=-2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_3\Rightarrow C'_3=-2 \)\[ \displaystyle x(0)=-2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_3\Rightarrow C'_3=-2 \];

Calculating the value of x(t) for t = 2 s and t = 4 s, using various values of
-
For C' = 0
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2=3,1\;\mathrm{m} \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2=3,1\;\mathrm{m} \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4=15,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4=15,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=15,9-3,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=15,9-3,1=12,8\;\mathrm m \]
-
For C' = 2
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times {\frac{2^2}{2}}+0,5\times 2+2=5,1\;\mathrm m \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times {\frac{2^2}{2}}+0,5\times 2+2=5,1\;\mathrm m \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+4\times 4+2=17,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+4\times 4+2=17,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=17,9-5,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=17,9-5,1=12,8\;\mathrm m \]
-
For C' = −2
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2-2=1,1\;\mathrm m \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2-2=1,1\;\mathrm m \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4-2=13,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4-2=13,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=13,9-1,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=13,9-1,1=12,8\;\mathrm m \]
For any other chosen instants (for example, 1 s and 7 s, or 12 s and 23 s, or 35 s and 100 s, etc.), the displacements will differ from 12.8 m, because the block is accelerated by the applied force. However, the displacements between those times will be the same for the same initial positions chosen.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .