Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
Se da la posición de una partícula que se mueve con velocidad constante en tres instantes diferentes:
\[
\begin{gather}
S = 6\;\mathrm m\quad\text{en}\quad t = 2\;\mathrm s\\
S = 9\;\mathrm m\quad\text{en}\quad t = 4\;\mathrm s\\
S = 33\;\mathrm m\quad\text{en}\quad t = 8\;\mathrm s\\
\end{gather}
\]
¿Cuál será la posición de la partícula en t = 10 s?
Datos del problema:
- En el instante t = 2 s la partícula está en la posición S = 6 m;
- En el instante t = 4 s la partícula está en la posición S = 9 m;
- En el instante t = 8 s la partícula está en la posición S = 33 m.
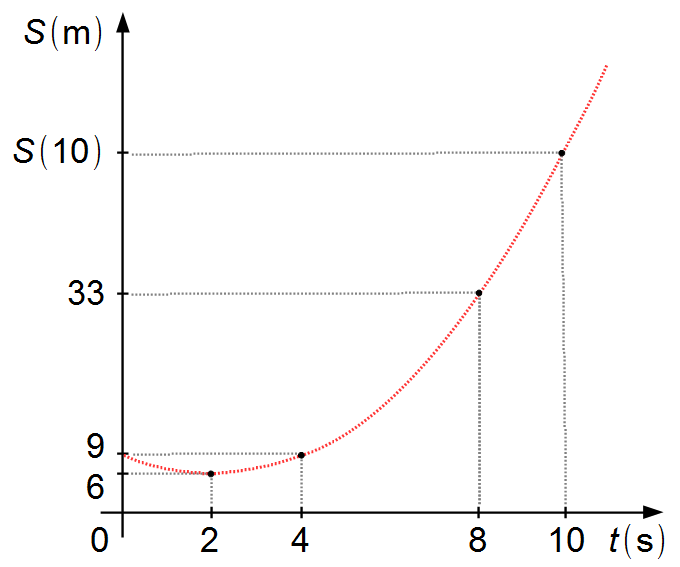
El problema nos da tres puntos en el plano
\( S\times t \)
y tenemos que determinar S(10). Para eso tenemos que encontrar la ecuación que pasa por esos
puntos. La partícula posee aceleración constante, está en
Movimiento Rectilíneo Uniformemente Variado (MRUV), que es dado por una parábola
(Gráfico 1).
Solución
La ecuación del movimiento con aceleración constante está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
escribiendo esta ecuación para los tres puntos dados, tenemos el siguiente sistema
\[
\begin{gather}
\left\{
\begin{matrix}
S_0+2v_0+\dfrac{a}{2}\times2^2=6\\
S_0+4v_0+\dfrac{a}{2}\times 4^2=9\\
S_0+8v_0+\dfrac{a}{2}\times 8^2=33
\end{matrix}
\right.\\[5pt]
\left\{
\begin{matrix}
S_0+2v_0+2a=6\\
S_0+4v_0+8a=9\\
S_0+8v_0+32a=33
\end{matrix}
\right.
\end{gather}
\]
este sistema puede ser representado por la siguiente matriz, donde los valores a la izquierda de la línea
discontinua representan la matriz de los coeficientes de la ecuación de movimiento y los valores a la derecha
representan los términos independientes
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2&\text{|}& 6\;\\
\;1& 4& 8&\text{|}& 9\;\\
\;1& 8& 32&\text{|}& 33\;
\end{matrix}
\right|
\end{gather}
\]
Para resolver el sistema, usamos el Método de Eliminación de Gauss.
Observación: El Método de Eliminación de Gauss para resolver este sistema consiste en
escalonar esta matriz de modo que se obtenga una matriz triangular superior. Para hacer el escalonamiento,
podemos realizar operaciones sobre las filas de la matriz, como multiplicar o dividir una fila entera
(incluyendo los términos independientes) por un número. También podemos sumar o restar una fila de otra y
podemos invertir dos filas de posición. Una matriz triangular superior es aquella en la que los elementos
debajo de la diagonal principal son todos nulos.
Para que el elemento a21 = 1 sea igual a cero, vamos restar la 1a fila de la 2a y sustituir la 2a fila \( \left(L_2-L_1\;\Rightarrow \;L_2\right) \)
\[
\begin{gather}
\qquad\qquad
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;1& 4& 8& \text{|}& 9\;\\
\;1& 8& 32& \text{|}&33\;
\end{matrix}
\right|\qquad L_2-L_1\;\Rightarrow \;L_2
\end{gather}
\]
- \( a_{21}=1-1=0 \);
- \( a_{22}=4-2=2 \);
- \( a_{23}=8-2=6 \);
- \( v_2=9-6=3 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;1& 8& 32&\text{|}& 33\;
\end{matrix}
\right|
\end{gather}
\]
Para que el elemento a31 = 1 sea igual a cero, vamos restar la 1a fila de la
3a y sustituir en la 3a fila
\( \left(L_3-L_1\;\Rightarrow \;L_3\right) \)
\[
\begin{gather}
\qquad \qquad
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;1& 8& 32& \text{|}&33\;
\end{matrix}
\right|
\qquad L_3-L_1\;\Rightarrow \;L_3
\end{gather}
\]
- \( a_{31}=1-1=0 \);
- \( a_{32}=8-2=6 \);
- \( a_{33}=32-2=30 \);
- \( v_3=33-6=27 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 6& 30&\text{|}& 27\;
\end{matrix}
\right|
\end{gather}
\]
Para que el elemento a32 = 6 sea igual a cero, vamos multiplicar la 2a fila por
3 y restar la 2a fila de la 3a y sustituir en la 3a fila
\( \left(L_3-3L_2\;\Rightarrow \;L_3\right) \)
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 6& 30&\text{|}&27\;
\end{matrix}
\right|
\qquad L_3-3L_2\;\Rightarrow \;L_3
\end{gather}
\]
- \( a_{31}=0-3\times 0=0 \);
- \( a_{32}=6-3\times 2=0 \);
- \( a_{33}=30-3\times 6-30=30-18=12 \);
- \( v_3=27-3\times 3=27-9=18 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 0& 12&\text{|}& 18\;
\end{matrix}
\right|
\end{gather}
\]
esta matriz representa el sistema
\[
\begin{gather}
\left\{
\begin{matrix}
S_0+2v_0+2a=6\\
\quad\quad\; 2v_0+6a=3\\
\qquad\qquad\quad 12a=18
\end{matrix}
\right.
\end{gather}
\]
ee inmediato, de la tercera ecuación tenemos
\[
\begin{gather}
12a=18\\[5pt]
a=\frac{\cancelto{3}{18}}{\cancelto{2}{12}}\\[5pt]
a=1,5\;\mathrm{m/s^2}
\end{gather}
\]
Sustituyendo el valor de a en la segunda ecuación del sistema
\[
\begin{gather}
2v_0+6\times 1,5=3\\[5pt]
2v_0+9=3\\[5pt]
v_0=\frac{3-9}{2}\\[5pt]
v_0=-3\;\mathrm{m/s}
\end{gather}
\]
Sustituyendo los valores de a y v0 en la primera ecuación del sistema
\[
\begin{gather}
S_0+2\times(-3)+2\times 1,5=6\\[5pt]
S_0-6+3=6\\[5pt]
S_0=6+3\\[5pt]
S_0=9\;\mathrm m
\end{gather}
\]
La ecuación de movimiento será
\[
\begin{gather}
S=9-3t+\frac{1,5}{2}t^2
\end{gather}
\]
para t = 10 s
\[
\begin{gather}
S=9-3\times 10+\frac{1,5}{2}\times10^2\\[5pt]
S=9-30+1,5\times 50
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S=54\;\mathrm m}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .