Exercício Resolvido de Movimento Unidimensional
publicidade
É dada a posição de uma partícula que se move com velocidade constante em três instantes diferentes:
\[
\begin{gather}
S = 6\;\mathrm m\quad\text{em}\quad t = 2\;\mathrm s\\
S = 9\;\mathrm m\quad\text{em}\quad t = 4\;\mathrm s\\
S = 33\;\mathrm m\quad\text{em}\quad t = 8\;\mathrm s\\
\end{gather}
\]
Qual será a posição da partícula em t = 10 s?
Dados do problema:
- No instante t = 2 s a partícula está na posição S = 6 m;
- No instante t = 4 s a partícula está na posição S = 9 m;
- No instante t = 8 s a partícula está na posição S = 33 m.
O problema nos dá três pontos no plano
\( S\times t \)
e temos que determinar S(10). Para isso temos que encontrar a equação que passa por esses pontos,
a partícula possui aceleração constante, está em Movimento Retilíneo Uniformemente Variado
(M.R.U.V.), que é dado por uma parábola (Gráfico 1).
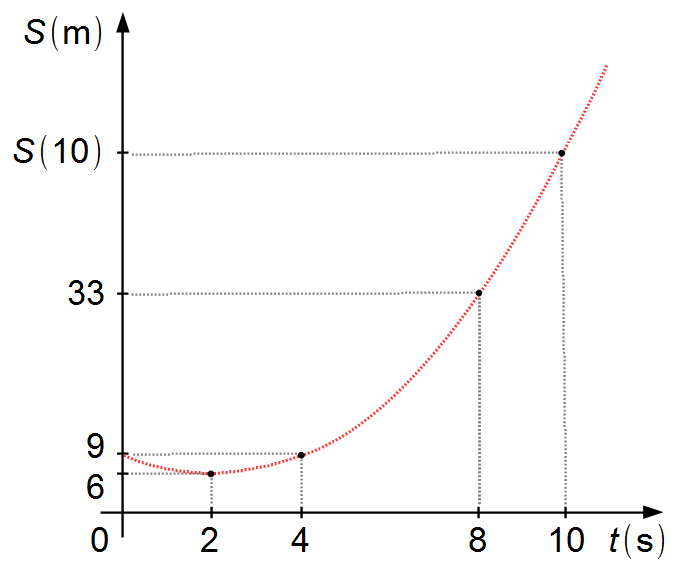
Solução
A equação do movimento com aceleração constante é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
escrevendo esta equação para os três pontos dados temos o seguinte sistema
\[
\begin{gather}
\left\{
\begin{matrix}
S_0+2v_0+\dfrac{a}{2}\times2^2=6\\
S_0+4v_0+\dfrac{a}{2}\times 4^2=9\\
S_0+8v_0+\dfrac{a}{2}\times 8^2=33
\end{matrix}
\right.\\[5pt]
\left\{
\begin{matrix}
S_0+2v_0+2a=6\\
S_0+4v_0+8a=9\\
S_0+8v_0+32a=33
\end{matrix}
\right.
\end{gather}
\]
este sistema pode ser representado pela matriz a seguir, onde os valores a esquerda da linha tracejada
representam a matriz dos coeficientes da equação de movimento e os valores a direita representam o vetor dos
termos independentes
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2&\text{|}& 6\;\\
\;1& 4& 8&\text{|}& 9\;\\
\;1& 8& 32&\text{|}& 33\;
\end{matrix}
\right|
\end{gather}
\]
Para resolver o sistema usamos o Método da Eliminação de Gauss.
Observação: O Método da Eliminação de Gauss para resolver este sistema consiste em
escalonar esta matriz de modo a obter uma matriz triangular superior. Para fazer o escalonamento podemos
realizar operações sobre as linhas da matriz como multiplicar ou dividir uma linha inteira (no caso
incluindo o vetor dos termos independentes) por um número, podemos somar ou subtrair uma linha de outra e
podemos inverter duas linhas de posição. Uma matriz triangular superior é aquela em que os elementos abaixo
da diagonal principal são todos nulos.
Para que o elemento a21 = 1 seja “zerado” vamos subtrair a 1.a linha da 2.a e substituir a 2.a linha \( \left(L_2-L_1\;\Rightarrow \;L_2\right) \)
\[
\begin{gather}
\qquad\qquad
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;1& 4& 8& \text{|}& 9\;\\
\;1& 8& 32& \text{|}&33\;
\end{matrix}
\right|\qquad L_2-L_1\;\Rightarrow \;L_2
\end{gather}
\]
- \( a_{21}=1-1=0 \);
- \( a_{22}=4-2=2 \);
- \( a_{23}=8-2=6 \);
- \( v_2=9-6=3 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;1& 8& 32&\text{|}& 33\;
\end{matrix}
\right|
\end{gather}
\]
Para que o elemento a31 = 1 seja “zerado” vamos subtrair a 1.a linha da
3.a e substituir na 3.a linha
\( \left(L_3-L_1\;\Rightarrow \;L_3\right) \)
\[
\begin{gather}
\qquad \qquad
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;1& 8& 32& \text{|}&33\;
\end{matrix}
\right|
\qquad L_3-L_1\;\Rightarrow \;L_3
\end{gather}
\]
- \( a_{31}=1-1=0 \);
- \( a_{32}=8-2=6 \);
- \( a_{33}=32-2=30 \);
- \( v_3=33-6=27 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 6& 30&\text{|}& 27\;
\end{matrix}
\right|
\end{gather}
\]
Para que o elemento a32 = 6 seja “zerado” vamos multiplicar a 2.a linha por 3 e
subtrair a 2.a linha da 3.a e substituir na 3.a linha
\( \left(L_3-3L_2\;\Rightarrow \;L_3\right) \)
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 6& 30&\text{|}&27\;
\end{matrix}
\right|
\qquad L_3-3L_2\;\Rightarrow \;L_3
\end{gather}
\]
- \( a_{31}=0-3\times 0=0 \);
- \( a_{32}=6-3\times 2=0 \);
- \( a_{33}=30-3\times 6-30=30-18=12 \);
- \( v_3=27-3\times 3=27-9=18 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 0& 12&\text{|}& 18\;
\end{matrix}
\right|
\end{gather}
\]
esta matriz representa o sistema
\[
\begin{gather}
\left\{
\begin{matrix}
S_0+2v_0+2a=6\\
\quad\quad\; 2v_0+6a=3\\
\qquad\qquad\quad 12a=18
\end{matrix}
\right.
\end{gather}
\]
de imediato da terceira equação temos
\[
\begin{gather}
12a=18\\[5pt]
a=\frac{\cancelto{3}{18}}{\cancelto{2}{12}}\\[5pt]
a=1,5\;\mathrm{m/s^2}
\end{gather}
\]
Substituindo o valor de a na segunda equação do sistema
\[
\begin{gather}
2v_0+6\times 1,5=3\\[5pt]
2v_0+9=3\\[5pt]
v_0=\frac{3-9}{2}\\[5pt]
v_0=-3\;\mathrm{m/s}
\end{gather}
\]
Substituindo os valores de a e v0 na primeira equação do sistema
\[
\begin{gather}
S_0+2\times(-3)+2\times 1,5=6\\[5pt]
S_0-6+3=6\\[5pt]
S_0=6+3\\[5pt]
S_0=9\;\mathrm m
\end{gather}
\]
A equação de movimento será
\[
\begin{gather}
S=9-3t+\frac{1,5}{2}t^2
\end{gather}
\]
para t = 10 s
\[
\begin{gather}
S=9-3\times 10+\frac{1,5}{2}\times10^2\\[5pt]
S=9-30+1,5\times 50
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S=54\;\mathrm m}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .