Solved Problem on One-dimensional Motion
advertisement
The position of a particle moving at a constant velocity is given at three different times:
\[
\begin{gather}
S = 6\;\mathrm m\quad\text{in}\quad t = 2\;\mathrm s\\
S = 9\;\mathrm m\quad\text{in}\quad t = 4\;\mathrm s\\
S = 33\;\mathrm m\quad\text{in}\quad t = 8\;\mathrm s\\
\end{gather}
\]
What will be the position of the particle at t = 10 s?
Problem data:
- At t = 2 s the particle is at position S = 6 m;
- At t = 4 s the particle is at position S = 9 m;
- At t = 8 s the particle is at position S = 33 m.
The problem gives us three points on the plane
\( S\times t \),
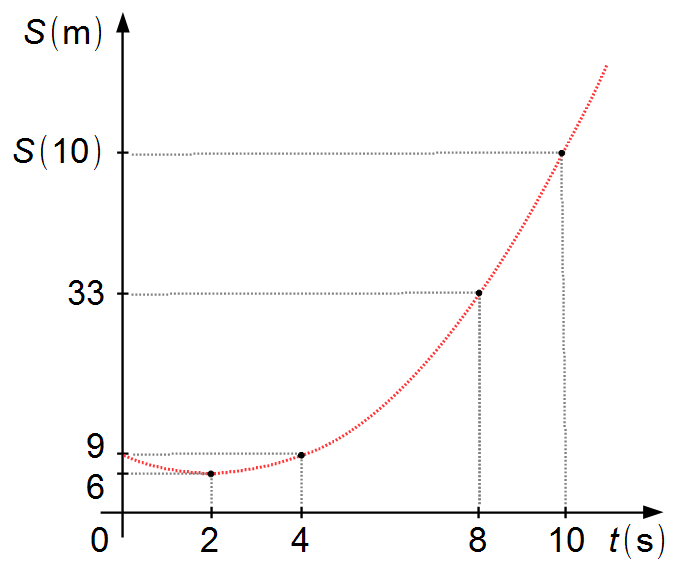
and we need to determine S(10). To do this, we need to find the equation that passes through these
points. The particle has constant acceleration and is in Uniformly Accelerated Rectilinear Motion,
represented by a parabola (Graph 1).
Solution
The equation of motion with constant acceleration is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
writing this equation for the three given points, we have the following system
\[
\begin{gather}
\left\{
\begin{matrix}
S_0+(2\;\mathrm s)v_0+\dfrac{a}{2}\times(2\;\mathrm s)^2=6\;\mathrm m\\
S_0+(4\;\mathrm s)v_0+\dfrac{a}{2}\times(4\;\mathrm s)^2=9\;\mathrm m\\
S_0+(8\;\mathrm s)v_0+\dfrac{a}{2}\times(8\;\mathrm s)^2=33\;\mathrm m
\end{matrix}
\right.\\[5pt]
\left\{
\begin{matrix}
S_0+(2\;\mathrm s)v_0+(2\;\mathrm s^2)a=6\;\mathrm m\\
S_0+(4\;\mathrm s)v_0+(8\;\mathrm s^2)a=9\;\mathrm m\\
S_0+(8\;\mathrm s)v_0+(32\;\mathrm s^2)a=33\;\mathrm m
\end{matrix}
\right.
\end{gather}
\]
this system can be represented by the following matrix, where the values to the left of the dashed line
represent the coefficient matrix of the equation of motion and the values to the right represent the vector
of the independent terms
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2&\text{|}& 6\;\\
\;1& 4& 8&\text{|}& 9\;\\
\;1& 8& 32&\text{|}& 33\;
\end{matrix}
\right|
\end{gather}
\]
To solve the system we use the Gaussian Elimination.
Note: The Gaussian Elimination for solving systems of linear equations consists of
performing elementary row operations to obtain an upper triangular matrix, then using back-substitution we
can find each unknown. To perform elementary operations on the rows of a matrix we can swap the position
of two rows, multiply an entire row by a non-zero scalar, and add one row to a multiple of another. An
upper triangular matrix is one where the entries below the main diagonal are zero.
To make the element a21 = 1 to be zero, we will subtract the 1st row from the 2nd row and substitute the 2nd row \( \left(L_2-L_1\;\Rightarrow \;L_2\right) \)
\[
\begin{gather}
\qquad\qquad
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;1& 4& 8& \text{|}& 9\;\\
\;1& 8& 32& \text{|}&33\;
\end{matrix}
\right|\qquad L_2-L_1\;\Rightarrow \;L_2
\end{gather}
\]
- \( a_{21}=1-1=0 \);
- \( a_{22}=4-2=2 \);
- \( a_{23}=8-2=6 \);
- \( v_2=9-6=3 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;1& 8& 32&\text{|}& 33\;
\end{matrix}
\right|
\end{gather}
\]
To make the element a31 = 1 to be zero, we will subtract the 1st row from the 3rd row and
substitute the 3rd row
\( \left(L_3-L_1\;\Rightarrow \;L_3\right) \)
\[
\begin{gather}
\qquad \qquad
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;1& 8& 32& \text{|}&33\;
\end{matrix}
\right|
\qquad L_3-L_1\;\Rightarrow \;L_3
\end{gather}
\]
- \( a_{31}=1-1=0 \);
- \( a_{32}=8-2=6 \);
- \( a_{33}=32-2=30 \);
- \( v_3=33-6=27 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 6& 30&\text{|}& 27\;
\end{matrix}
\right|
\end{gather}
\]
To make the element a32 = 6 to be zero, we will multiply the 2nd row by 3 and subtract the
2nd row from the 3rd row, then substitute the 3rd row
\( \left(L_3-3L_2\;\Rightarrow \;L_3\right) \)
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 6& 30&\text{|}&27\;
\end{matrix}
\right|
\qquad L_3-3L_2\;\Rightarrow \;L_3
\end{gather}
\]
- \( a_{31}=0-3\times 0=0 \);
- \( a_{32}=6-3\times 2=0 \);
- \( a_{33}=30-3\times 6-30=30-18=12 \);
- \( v_3=27-3\times 3=27-9=18 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 0& 12&\text{|}& 18\;
\end{matrix}
\right|
\end{gather}
\]
this matrix represents the system
\[
\begin{gather}
\left\{
\begin{matrix}
S_0+(2\;\mathrm s)v_0+(2\;\mathrm s^2)a=6\;\mathrm m\\
\quad\quad\; (2\;\mathrm s)v_0+(6\;\mathrm s^2)a=3\;\mathrm m\\
\qquad\qquad\qquad\; (12\;\mathrm s^2)a=18\;\mathrm m
\end{matrix}
\right.
\end{gather}
\]
immediately, from the third equation, we have
\[
\begin{gather}
(12\;\mathrm s^2)a=18\;\mathrm m\\[5pt]
a=\frac{\cancelto{3}{18}\;\mathrm m}{\cancelto{2}{12}\;\mathrm s^2}\\[5pt]
a=1.5\;\mathrm{m/s^2}
\end{gather}
\]
Substituting the value of a into the second equation of the system
\[
\begin{gather}
(2\;\mathrm s)v_0+\left(6\;\mathrm{\cancel{s^2}}\right)\times\left(1.5\;\mathrm{\frac{m}{\cancel{s^2}}}\right)=3\;\mathrm m\\[5pt]
(2\;\mathrm s)v_0+9\;\mathrm m=3\;\mathrm m\\[5pt]
v_0=\frac{(3-9)\;\mathrm m}{2\;\mathrm s}\\[5pt]
v_0=-3\;\mathrm{m/s}
\end{gather}
\]
Substituting the values of a and v0 into the first equation of the system
\[
\begin{gather}
S_0+(2\;\mathrm{\cancel s})\times\left(-3\;\mathrm{\frac{m}{\cancel s}}\right)+(2\;\mathrm{\cancel{s^2}})\times\left(1.5\;\mathrm{\frac{m}{\cancel{s^2}}}\right)=6\;\mathrm m\\[5pt]
S_0-6\;\mathrm m+3\;\mathrm m=6\;\mathrm m\\[5pt]
S_0=(6+3)\;\mathrm m\\[5pt]
S_0=9\;\mathrm m
\end{gather}
\]
The equation of motion will be
\[
\begin{gather}
S=9\;\mathrm m-\left(3\;\mathrm{\frac{m}{s}}\right)t+\frac{1.5\;\mathrm{\frac{m}{s^2}}}{2}t^2
\end{gather}
\]
for t = 10 s
\[
\begin{gather}
S=9\;\mathrm m-\left(3\;\mathrm{\frac{m}{\cancel s}}\right)\times(10\;\mathrm{\cancel s})+\frac{1.5\;\mathrm{\frac{m}{s^2}}}{2}\times(10\;\mathrm s)^2\\[5pt]
S=9\;\mathrm m-3\;\mathrm m+\left(1.5\;\mathrm{\frac{m}{\cancel{s^2}}}\right)\times(50\;\mathrm{\cancel{s^2}})\\[5pt]
S=9\;\mathrm m-30\;\mathrm m+1.5\;\mathrm m\times 50
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S=54\;\mathrm m}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .