Exercice Résolu sur les Mouvement Unidimensionnel
publicité
On donne la position d'une particule qui se déplace à vitesse constante à trois instants différents:
\[
\begin{gather}
S = 6\;\mathrm m\quad\text{en}\quad t = 2\;\mathrm s\\
S = 9\;\mathrm m\quad\text{en}\quad t = 4\;\mathrm s\\
S = 33\;\mathrm m\quad\text{en}\quad t = 8\;\mathrm s\\
\end{gather}
\]
Quelle sera la position de la particule à t = 10 s?
Dados do problema:
- À l'instant t = 2 s la particule est à la position S = 6 m;
- À l'instant t = 4 s la particule est à la position S = 9 m;
- À l'instant t = 8 s la particule est à la position S = 33 m.
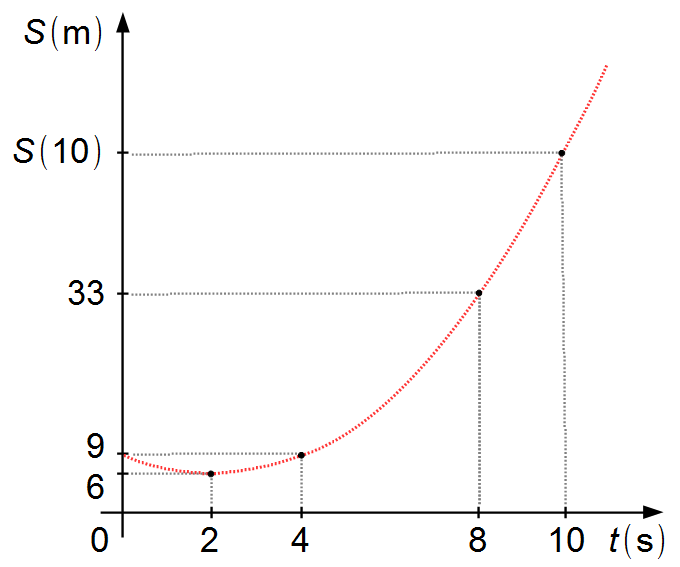
Le problème nous donne trois points dans le plan
\( S\times t \)
et nous devons déterminer S(10). Pour cela, nous devons trouver l'équation qui passe par ces
points. La particule possède une accélération constante, elle est en
Mouvement Rectiligne Uniformément Varié (MRUV), qui est donné par une parabole
(Graphique 1).
Solution
L'équation du mouvement avec accélération constante est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
en écrivant cette équation pour les trois points donnés, nous avons le système suivant
\[
\begin{gather}
\left\{
\begin{matrix}
S_0+2v_0+\dfrac{a}{2}\times2^2=6\\
S_0+4v_0+\dfrac{a}{2}\times 4^2=9\\
S_0+8v_0+\dfrac{a}{2}\times 8^2=33
\end{matrix}
\right.\\[5pt]
\left\{
\begin{matrix}
S_0+2v_0+2a=6\\
S_0+4v_0+8a=9\\
S_0+8v_0+32a=33
\end{matrix}
\right.
\end{gather}
\]
ce système peut être représenté par la matrice suivante, où les valeurs à gauche de la ligne pointillée
représentent la matrice des coefficients de l'équation de mouvement et les valeurs à droite représentent le
vecteur colonne.
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2&\text{|}& 6\;\\
\;1& 4& 8&\text{|}& 9\;\\
\;1& 8& 32&\text{|}& 33\;
\end{matrix}
\right|
\end{gather}
\]
Pour résoudre le système, nous utilisons la Méthode de l'Élimination de Gauss.
Remarque: La Méthode de l'Élimination de Gauss pour résoudre ce système consiste à
obtenir la matrice sous forme échelonnée réduite. Pour obtenir une matrice triangulaire inférieure, nous
pouvons effectuer des opérations sur les lignes de la matrice telles que multiplier ou diviser une ligne
entière (dans ce cas, y compris le vecteur colonne) par un nombre, nous pouvons additionner ou soustraire
une ligne d'une autre et nous pouvons échanger la position de deux lignes. Une matrice triangulaire
supérieure est celle où les éléments sous la diagonale principale sont tous nuls.
Pour que l'élément a21 = 1 soit annulé, nous allons soustraire la 1ère ligne de la 2ème et remplacer la 2ème ligne \( \left(L_2-L_1\;\Rightarrow \;L_2\right) \)
\[
\begin{gather}
\qquad\qquad
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;1& 4& 8& \text{|}& 9\;\\
\;1& 8& 32& \text{|}&33\;
\end{matrix}
\right|\qquad L_2-L_1\;\Rightarrow \;L_2
\end{gather}
\]
- \( a_{21}=1-1=0 \);
- \( a_{22}=4-2=2 \);
- \( a_{23}=8-2=6 \);
- \( v_2=9-6=3 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;1& 8& 32&\text{|}& 33\;
\end{matrix}
\right|
\end{gather}
\]
Pour que l'élément a31 = 1 soit annulé, nous allons soustraire la 1ère ligne de la 3ème et
remplacer dans la 3ème ligne
\( \left(L_3-L_1\;\Rightarrow \;L_3\right) \)
\[
\begin{gather}
\qquad \qquad
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;1& 8& 32& \text{|}&33\;
\end{matrix}
\right|
\qquad L_3-L_1\;\Rightarrow \;L_3
\end{gather}
\]
- \( a_{31}=1-1=0 \);
- \( a_{32}=8-2=6 \);
- \( a_{33}=32-2=30 \);
- \( v_3=33-6=27 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 6& 30&\text{|}& 27\;
\end{matrix}
\right|
\end{gather}
\]
Pour que l'élément a32 = 6 soit annulé, nous allons multiplier la 2ème ligne par 3 et
soustraire la 2ème ligne de la 3ème et remplacer dans la 3ème ligne
\( \left(L_3-3L_2\;\Rightarrow \;L_3\right) \)
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 6& 30&\text{|}&27\;
\end{matrix}
\right|
\qquad L_3-3L_2\;\Rightarrow \;L_3
\end{gather}
\]
- \( a_{31}=0-3\times 0=0 \);
- \( a_{32}=6-3\times 2=0 \);
- \( a_{33}=30-3\times 6-30=30-18=12 \);
- \( v_3=27-3\times 3=27-9=18 \).
\[
\begin{gather}
\left|
\begin{matrix}
\;1& 2& 2& \text{|}& 6\;\\
\;0& 2& 6& \text{|}& 3\;\\
\;0& 0& 12&\text{|}& 18\;
\end{matrix}
\right|
\end{gather}
\]
cette matrice représente le système
\[
\begin{gather}
\left\{
\begin{matrix}
S_0+2v_0+2a=6\\
\quad\quad\; 2v_0+6a=3\\
\qquad\qquad\quad 12a=18
\end{matrix}
\right.
\end{gather}
\]
immédiatement, de la troisième équation, nous avons
\[
\begin{gather}
12a=18\\[5pt]
a=\frac{\cancelto{3}{18}}{\cancelto{2}{12}}\\[5pt]
a=1,5\;\mathrm{m/s^2}
\end{gather}
\]
En substituant la valeur de a dans la deuxième équation du système
\[
\begin{gather}
2v_0+6\times 1,5=3\\[5pt]
2v_0+9=3\\[5pt]
v_0=\frac{3-9}{2}\\[5pt]
v_0=-3\;\mathrm{m/s}
\end{gather}
\]
En substituant les valeurs de a et v0 dans la première équation du système
\[
\begin{gather}
S_0+2\times(-3)+2\times 1,5=6\\[5pt]
S_0-6+3=6\\[5pt]
S_0=6+3\\[5pt]
S_0=9\;\mathrm m
\end{gather}
\]
L'équation du mouvement sera
\[
\begin{gather}
S=9-3t+\frac{1,5}{2}t^2
\end{gather}
\]
pour t = 10 s
\[
\begin{gather}
S=9-3\times 10+\frac{1,5}{2}\times10^2\\[5pt]
S=9-30+1,5\times 50
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S=54\;\mathrm m}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .