Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
Una piedra es lanzada, con una velocidad inicial de 15 m/s, desde lo alto de un acantilado de 20 m de altura, simultáneamente, otra piedra es lanzada verticalmente desde la parte inferior del acantilado hacia arriba, también con una velocidad de 15 m/s. Determina:
a) ¿Después de cuánto tiempo y a qué altura se cruzan las piedras?
b) ¿La piedra lanzada desde abajo alcanza la parte superior del acantilado?
Datos del problema:
- Altura del acantilado: h = 20 m;
- Velocidad de la piedra lanzada hacia abajo: v01 = 15 m/s;
- Velocidad de la piedra lanzada hacia abajo: v02 = 15 m/s;
- Aceleración de la gravedad: g = 9,8 m/s2.
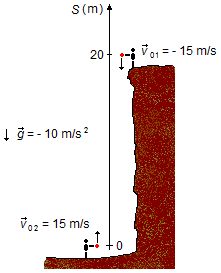
Tomamos un sistema de referencia orientado hacia arriba con origen en el punto más bajo desde donde se
lanza la piedra hacia arriba. La aceleración de la gravedad y la velocidad de la piedra lanzada desde lo
alto del acantilado están orientadas en sentido contrario a la trayectoria y son negativas,
v01 = −15 m/s, g = −9,8 m/s2. Dado que la piedra se lanza
desde lo alto del acantilado, su posición inicial será S01 = 20 m. La piedra lanzada
desde abajo tiene su velocidad en el mismo sentido de la trayectoria, es positiva
v02 = 15 m/s, y dado que está en el origen, su posición inicial será
S02 = 0 (Figura 1).
Solución
a) Los movimientos de caída libre y lanzamiento vertical están dados por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t-\frac{g}{2}t^2}
\end{gather}
\]
Las ecuaciones horarias para las piedras serán
\[
\begin{gather}
S_1=S_{01}+v_{01}t-\frac{g}{2}t^2\\[5pt]
S_1=20-15t-\frac{9,8}{2}t^2\\[5pt]
S_1=20-15t-4,9t^2 \tag{I}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_{02}t-\frac{g}{2}t^2\\[5pt]
S_2=0+15t-\frac{9,8}{2}t^{2}\\[5pt]
S_2=15t-4,9t^{2} \tag{II}
\end{gather}
\]
Cuando las piedras se encuentran, tenemos la condición de que sus posiciones son iguales, igualando las
ecuaciones (I) y (II)
\[
\begin{gather}
S_1=S_2\\[5pt]
20-15t-4,9t^2=15t-4,9t^2\\[5pt]
20=15t+4,9t^{2}+15t-4,9t^{2}\\[5pt]
30t=20\\[5pt]
t=\frac{2 \cancel 0}{3 \cancel 0}\\[5pt]
t=\frac{2}{3} \tag{III}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t\;\approx \;0,67\;\mathrm s}
\end{gather}
\]
Para encontrar el punto de encuentro de las piedras, vamos a sustituir el intervalo de tiempo, encontrado en
la forma de la expresión (III), en la ecuación (II)
\[
\begin{gather}
S_2=\cancelto{5}{15}\times\frac{2}{\cancel 3}-5\times\left(\frac{2}{3}\right)^2\\[5pt]
S_2=5\times 2-5\times\frac{4}{9}\\[5pt]
S_2=10-\frac{20}{9}
\end{gather}
\]
multiplicando y dividiendo por 9 el primer término del lado derecho de la igualdad
\[
\begin{gather}
S_2=10\times\frac{9}{9}-\frac{20}{9}\\[5pt]
S_2=\frac{90}{9}-\frac{20}{9}\\[5pt]
S_2=\frac{70}{9}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_2\approx 7,8\;\mathrm m}
\end{gather}
\]
Observación: si sustituyéramos el intervalo de tiempo en la ecuación (I), obtendríamos el
mismo resultado, ya que es el punto de la trayectoria donde las piedras se cruzan.
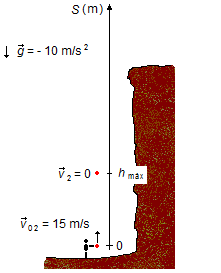
b) Cuando la piedra lanzada desde abajo alcanza su altura máxima, hmáx, se detiene por
un instante y su velocidad se anula, v2 = 0, antes de comenzar a caer (Figura 2).
Aplicando la ecuación de la velocidad en función de la aceleración y el desplazamiento
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v^2=v_0^2-2g\Delta S}
\end{gather}
\]
donde ΔS = hmáx
\[
\begin{gather}
v_2^2=v_{02}^2-2gh_{max}\\[5pt]
h_{max}=\frac{v_{02}^2-v_2^2}{2g}\\[5pt]
h_{max}=\frac{15^2-0^2}{2\times 9,8}\\[5pt]
h_{max}=\frac{225}{19,6}\\[5pt]
h_{max}\approx 11,5\;\mathrm{m}
\end{gather}
\]
La piedra lanzada desde abajo no alcanza la parte superior
del acantilado.
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .