Solved Problem on One-dimensional Motion
advertisement
A stone is thrown, at an initial speed of 15 m/s from the top of a 20 m high cliff, while another stone is thrown vertically from the bottom of the cliff upwards also at a speed of 15 m/s. Determine:
a) After how long and at what height do the stones intersect?
b) Does the stone throw from below reach the top of the cliff?
Problem data:
- Height of the cliff: h = 20 m;
- Speed of the stone thrown down: v01 = 15 m/s;
- Speed of the stone thrown up: v02 = 15 m/s;
- Acceleration due to gravity: g = 9,8 m/s2.
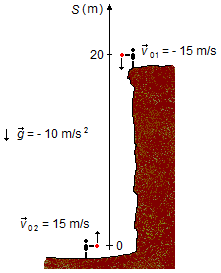
We chose a reference frame at the lower part of the cliff pointed upward. The acceleration due to
gravity and the velocity of the stone thrown from the cliff are in the opposite direction of the
reference frame and are negative (v01 = −15 m/s,
g = −9,8 m/s2), the stone thrown from the top of the cliff has an initial
position S01 = 20 m. The stone thrown from below has its velocity in the same
direction of the coordinate system, positive (v02 = 15 m/s), as it is at the origin
its initial position will be S02 = 0 (Figure 1).
Solution
a) The equation for free-fall is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t-\frac{g}{2}t^2}
\end{gather}
\]
The equation of displacement as a function of time for both stones will be
\[
\begin{gather}
S_1=S_{01}+v_{01}t-\frac{g}{2}t^2\\[5pt]
S_1=20\;\mathrm m-\left(15\;\mathrm{\small{\frac{m}{s}}}\right)t-\left(\frac{9,8\;\mathrm{\frac{m}{s^2}}}{2}\right)t^2\\[5pt]
S_1=20\;\mathrm m-\left(15\;\mathrm{\small{\frac{m}{s}}}\right)t-\left(4,9\;\mathrm{\frac{m}{s^2}}\right)t^2 \tag{I}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_{02}t-\frac{g}{2}t^2\\[5pt]
S_2=0+\left(15\;\mathrm{\small{\frac{m}{s}}}\right)t-\left(\frac{9,8\;\mathrm{\frac{m}{s^2}}}{2}\right)t^2\\[5pt]
S_2=\left(15\;\mathrm{\small{\frac{m}{s}}}\right)t-\left(4,9\;\mathrm{\frac{m}{s^2}}\right)t^2 \tag{II}
\end{gather}
\]
When the stones intersect, we have the condition that their positions are equal, equating equations (I)
and (II)
\[
\begin{gather}
S_1=S_2\\[5pt]
20\;\mathrm m-\left(15\;\mathrm{\small{\frac{m}{s}}}\right)t-\left(4,9\;\mathrm{\frac{m}{s^2}}\right)t^2=\left(15\;\mathrm{\small{\frac{m}{s}}}\right)t-\left(4,9\;\mathrm{\frac{m}{s^2}}\right)t^2\\[5pt]
20\;\mathrm m=\left(15\;\mathrm{\small{\frac{m}{s}}}\right)t+\left(4,9\;\mathrm{\frac{m}{s^2}}\right)t^2+\left(15\;\mathrm{\small{\frac{m}{s}}}\right)t-\left(4,9\;\mathrm{\frac{m}{s^2}}\right)t^2\\[5pt]
\left(30\;\mathrm{\small{\frac{m}{s}}}\right)t=20\;\mathrm m\\[5pt]
t=\frac{2\cancel 0\;\mathrm{\cancel m}}{3\cancel 0\;\mathrm{\frac{\cancel m}{s}}}\\[5pt]
t=\frac{2}{3}\;\mathrm s \tag{III}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t\;\approx \;0.67\;\mathrm s}
\end{gather}
\]
To find the intersecting point of the stones, we will substitute the time found in the form of expression
(III) into equation (II)
\[
\begin{gather}
S_2=\left(\cancelto{5}{15}\;\mathrm{\small{\frac{m}{\cancel s}}}\right)\left(\frac{2}{\cancel 3}\;\mathrm{\cancel s}\right)-\left(4,9\;\mathrm{\small{\frac{m}{s^2}}}\right)\left(\frac{2}{3}\;\mathrm s\right)^2\\[5pt]
S_2=(5\;\mathrm m)\times 2-\left(4,9\;\mathrm{\small{\frac{m}{\cancel{s^2}}}}\right)\left(\frac{4}{9}\;\mathrm{\cancel{s^2}}\right)\\[5pt]
S_2=10\;\mathrm m-\frac{19,6}{9}\;\mathrm m
\end{gather}
\]
multiplying and dividing by 9 the first term on the right-had side
\[
\begin{gather}
S_2=(10\;\mathrm m)\times\frac{9}{9}-\frac{20}{9}\;\mathrm m\\[5pt]
S_2=\frac{90}{9}\;\mathrm m)-\frac{19,6}{9}\;\mathrm m\\[5pt]
S_2=\frac{70,4}{9}\;\mathrm m
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_2\approx 7.8\;\mathrm m}
\end{gather}
\]
Note: if we substitute the time in the equation (I), we would obtain the same result since
it is the point of the trajectory where the stones intersect.
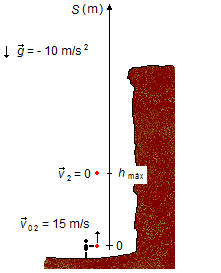
b) When the stone was thrown from below reaches its maximum height, hmáx, it stops for
an instant, and its speed is equal to zero, v2 = 0 before it begins to fall (figure 2).
Using the equation of velocity as a function of displacement
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v^2=v_0^2-2g\Delta S}
\end{gather}
\]
where ΔS = hmáx
\[
\begin{gather}
v_2^2=v_{02}^2-2gh_{max}\\[5pt]
h_{max}=\frac{v_{02}^2-v_2^2}{2g}\\[5pt]
h_{max}=\frac{\left(15\;\mathrm{\frac{m}{s}}\right)^2-0^2}{2\times\left(9,8\;\mathrm{\frac{m}{s^2}}\right)}\\[5pt]
h_{max}=\frac{225\;\mathrm{\frac{m^\cancel 2}{\cancel{s^2}}}}{19,6\;\mathrm{\frac{\cancel m}{\cancel{s^2}}}}\\[5pt]
h_{max}\approx 11.5\;\mathrm m
\end{gather}
\]
The stone thrown from below does not reach the top of the
cliff.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .