Exercice Résolu sur les Mouvement Unidimensionnel
publicité
Une pierre est lancée, avec une vitesse initiale de 15 m/s, du sommet d'une falaise de 20 m de hauteur, simultanément une autre pierre est lancée verticalement depuis le bas de la falaise vers le haut également avec une vitesse de 15 m/s. Déterminer:
a) Après combien de temps et à quelle hauteur les pierres se croisent-elles ?
b) La pierre lancée d'en bas atteint-elle le sommet de la falaise?
Données du problème:
- Hauteur de la falaise: h = 20 m;
- Vitesse de la pierre lancée vers le bas: v01 = 15 m/s;
- Vitesse de la pierre lancée vers le haut: v02 = 15 m/s;
- Accélération de la pesanteur: g = 9,8 m/s2.
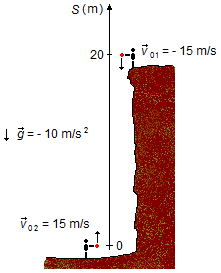
Nous choisissons un système de référentiel orienté vers le haut avec l'origine au point le plus bas d'où
la pierre est lancée vers le haut. L'accélération de la peanteur et la vitesse de la pierre lancée du
haut de la falaise sont orientées dans le sens opposé de la trajectoire et sont négatives,
v01 = −15 m/s, g = −9,8 m/s2. Comme la pierre est lancée
du haut de la falaise, sa position initiale sera S01 = 20 m. La pierre lancée d'en bas
a sa vitesse dans le même sens que la trajectoire, elle est positive v02 = 15 m/s, et
comme elle est à l'origine, sa position initiale sera S02 = 0 (Figure 1).
Solution
a) Les mouvements de chute libre et de lancement vertical sont donnés par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t-\frac{g}{2}t^2}
\end{gather}
\]
Les équations horaires pour les pierres seront
\[
\begin{gather}
S_1=S_{01}+v_{01}t-\frac{g}{2}t^2\\[5pt]
S_1=20-15t-\frac{9,8}{2}t^2\\[5pt]
S_1=20-15t-4,9t^2 \tag{I}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_{02}t-\frac{g}{2}t^2\\[5pt]
S_2=0+15t-\frac{9,8}{2}t^{2}\\[5pt]
S_2=15t-4,9t^{2} \tag{II}
\end{gather}
\]
Lorsque les pierres se rencontrent, nous avons la condition que leurs positions sont égales, en égalant les
équations (I) et (II)
(I) e (II)
\[
\begin{gather}
S_1=S_2\\[5pt]
20-15t-4,9t^2=15t-4,9t^2\\[5pt]
20=15t+4,9t^{2}+15t-4,9t^{2}\\[5pt]
30t=20\\[5pt]
t=\frac{2 \cancel 0}{3 \cancel 0}\\[5pt]
t=\frac{2}{3} \tag{III}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t\;\approx \;0,67\;\mathrm s}
\end{gather}
\]
Pour trouver le point de rencontre des pierres, nous allons substituer l'intervalle de temps, trouvé sous la
forme de l'expression (III), dans l'équation (II)
\[
\begin{gather}
S_2=\cancelto{5}{15}\times\frac{2}{\cancel 3}-5\times\left(\frac{2}{3}\right)^2\\[5pt]
S_2=5\times 2-5\times\frac{4}{9}\\[5pt]
S_2=10-\frac{20}{9}
\end{gather}
\]
En multipliant et en divisant par 9 le premier terme du côté droit de l'égalité
\[
\begin{gather}
S_2=10\times\frac{9}{9}-\frac{20}{9}\\[5pt]
S_2=\frac{90}{9}-\frac{20}{9}\\[5pt]
S_2=\frac{70}{9}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_2\approx 7,8\;\mathrm m}
\end{gather}
\]
Remarque: si nous substituions l'intervalle de temps dans l'équation (I), nous obtiendrions
le même résultat, car c'est le point de la trajectoire où les pierres se croisent.
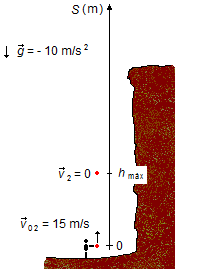
b) Lorsque la pierre lancée d'en bas atteint sa hauteur maximale, hmáx, elle s'arrête
brièvement et sa vitesse s'annule, v2 = 0, avant de commencer à tomber (Figure 2). En
appliquant l'équation de la vitesse en fonction de l'accélération et du déplacement
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v^2=v_0^2-2g\Delta S}
\end{gather}
\]
où ΔS = hmáx
\[
\begin{gather}
v_2^2=v_{02}^2-2gh_{max}\\[5pt]
h_{max}=\frac{v_{02}^2-v_2^2}{2g}\\[5pt]
h_{max}=\frac{15^2-0^2}{2\times 9,8}\\[5pt]
h_{max}=\frac{225}{19,6}\\[5pt]
h_{max}\approx 11,5\;\mathrm{m}
\end{gather}
\]
La pierre lancée d'en bas n'atteint pas le sommet de la
falaise
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .