Exercício Resolvido de Movimento Unidimensional
publicidade
Uma pedra é jogada, com velocidade inicial de 15 m/s, do alto de um penhasco de 20 m de altura, simultaneamente uma outra pedra é lançada verticalmente da parte inferior do penhasco para cima também com velocidade de 15 m/s. Determine:
a) Depois de quanto tempo e a que altura as pedras se cruzam?
b) A pedra lançada de baixo atinge o alto do penhasco?
Dados do problema:
- Altura do penhasco: h = 20 m;
- Velocidade da pedra jogada para baixo: v01 = 15 m/s;
- Velocidade da pedra lanada para cima: v02 = 15 m/s;
- Aceleração da gravidade: g = 9,8 m/s2.
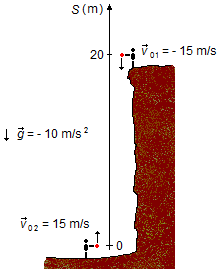
Adotamos um sistema de referência orientado para cima com origem na parte mais baixa de onde é lançada
a pedra para cima. A aceleração da gravidade e a velocidade da pedra jogada de cima do penhasco
estão orientadas no sentido contrário da trajetória e são negativas,
v01 = −15 m/s, g = −9,8 m/s2, como a pedra é lançada do
alto do penhasco sua posição inicial será S01 = 20 m. A pedra lançada de baixo tem sua
velocidade no mesmo sentido da trajetória, é positiva v02 = 15 m/s, como ela está na
origem sua posição inicial será S02 = 0 (Figura 1).
Solução
a) Os movimentos de queda livre e lançamento vertical são dados por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t-\frac{g}{2}t^2}
\end{gather}
\]
As equaçóes horárias para as pedras serão
\[
\begin{gather}
S_1=S_{01}+v_{01}t-\frac{g}{2}t^2\\[5pt]
S_1=20-15t-\frac{9,8}{2}t^2\\[5pt]
S_1=20-15t-4,9t^2 \tag{I}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_{02}t-\frac{g}{2}t^2\\[5pt]
S_2=0+15t-\frac{9,8}{2}t^{2}\\[5pt]
S_2=15t-4,9t^{2} \tag{II}
\end{gather}
\]
Quando as pedras se encontram temos a condição de que suas posições são iguais, igualando as equações
(I) e (II)
\[
\begin{gather}
S_1=S_2\\[5pt]
20-15t-4,9t^2=15t-4,9t^2\\[5pt]
20=15t+4,9t^{2}+15t-4,9t^{2}\\[5pt]
30t=20\\[5pt]
t=\frac{2 \cancel 0}{3 \cancel 0}\\[5pt]
t=\frac{2}{3} \tag{III}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t\;\approx \;0,67\;\mathrm s}
\end{gather}
\]
Para encontrarmos o ponto de encontro das pedras vamos substituir o intervalo de tempo, encontrado na forma
da expressão (III) na equação (II)
\[
\begin{gather}
S_2=\cancelto{5}{15}\times\frac{2}{\cancel 3}-5\times\left(\frac{2}{3}\right)^2\\[5pt]
S_2=5\times 2-5\times\frac{4}{9}\\[5pt]
S_2=10-\frac{20}{9}
\end{gather}
\]
multiplicando e dividindo por 9 o primeiro termo do lado direito da igualdade
\[
\begin{gather}
S_2=10\times\frac{9}{9}-\frac{20}{9}\\[5pt]
S_2=\frac{90}{9}-\frac{20}{9}\\[5pt]
S_2=\frac{70}{9}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_2\approx 7,8\;\mathrm m}
\end{gather}
\]
Observação: se substituíssemos o intervalo de tempo na equação (I) obteríamos o mesmo
resultado, já que é o ponto da trajetória onde as pedras se cruzam.
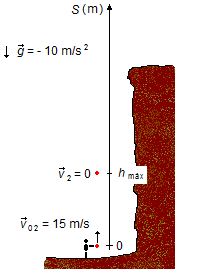
b) Quando a pedra lançada de baixo atinge sua altura máxima, hmáx, ela para por um
instante e sua velocidade se anula, v2 = 0, antes de começar a cair (Figura 2).
Aplicando a Equação de Torricelli
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v^2=v_0^2-2g\Delta S}
\end{gather}
\]
onde ΔS = hmáx
\[
\begin{gather}
v_2^2=v_{02}^2-2gh_{max}\\[5pt]
h_{max}=\frac{v_{02}^2-v_2^2}{2g}\\[5pt]
h_{max}=\frac{15^2-0^2}{2\times 9,8}\\[5pt]
h_{max}=\frac{225}{19,6}\\[5pt]
h_{max}\approx 11,5\;\mathrm{m}
\end{gather}
\]
A pedra lançada de baixo não atinge o alto do penhasco.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .