Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
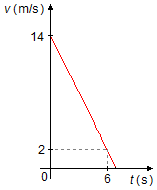
El movimiento de un cuerpo está descrito por el gráfico de la velocidad en función del tiempo como se
muestra en la figura. Determine:
a) La aceleración del cuerpo;
b) Escribir la ecuación horaria de la velocidad;
c) ¿Cuál es el espacio recorrido entre 3 s y 7 s?
a) La aceleración del cuerpo;
b) Escribir la ecuación horaria de la velocidad;
c) ¿Cuál es el espacio recorrido entre 3 s y 7 s?
Solución
a) Tomamos dos puntos del gráfico, (x1, y1) = (6, 2) y
(x2, y2) = (0, 14). La aceleración del cuerpo, en un gráfico
de velocidad en función del tiempo (v × t), estará dada por la tangente de la recta
(Figura 1).
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a=\operatorname{tg}\alpha =-\operatorname{tg}\beta=\frac{\text{cateto opuesto}}{\text{cateto adyacente}}=\frac{v_2-v_1}{t_2-t_1}}
\end{gather}
\]
\[
\begin{gather}
a=\frac{14-2}{0-6}\\[5pt]
a=\frac{12}{-6}
\end{gather}
\]
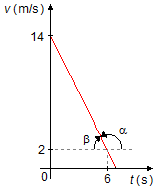
Figura 1
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a=-2\;\mathrm{m/s^2}}
\end{gather}
\]
b) La recta representa el gráfico de una Función Lineal del tipo \( y=ax+b \). Comparando con la función para la velocidad del Movimiento Rectilíneo Uniformemente Variado (MRUV), podemos hacer las siguientes asociaciones
\[
\begin{array}{c}
y & = & b & + & a x\\
\downarrow & & \downarrow & & \downarrow & \\
v & = & v_0 & + & a t
\end{array}
\]
la constante a fue obtenido en el ítem anterior y corresponde a la aceleración
a = −2 m/s2, y el valor de b corresponde a la velocidad inicial del cuerpo
que se lee en el gráfico donde la recta corta el eje de las ordenadas como siendo v0 = 14 m.
La ecuación horaria de la velocidad será
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=14-2t}
\end{gather}
\]
c) En primer lugar, debemos determinar las velocidades del cuerpo en los instantes 3 y 7 segundos usando la expresión para la velocidad obtenida en el ítem anterior
- Para t = 3 s
\[
\begin{gather}
v(3)=14-2\times 3\\[5pt]
v(3)=14-6\\[5pt]
v(3)=8\;\mathrm{m/s}
\end{gather}
\]
- Para t = 7 s
\[
\begin{gather}
v(7)=14-2\times 7\\[5pt]
v(7)=14-14\\[5pt]
v(7)=0
\end{gather}
\]
En un gráfico de velocidad en función del tiempo v × t, el espacio recorrido es
igual al área bajo la curva (Figura 2). La área de un triángulo está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A=\frac{Bh}{2}}
\end{gather}
\]
el espacio recorrido será
\[
\begin{gather}
\Delta S=A=\frac{(7-3)\times \cancelto{4}{8}}{\cancel 2}\\[5pt]
\Delta S=4\times 4
\end{gather}
\]
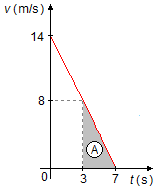
Figura 2
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta S=16\;\mathrm{m/s}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .