Solved Problem on One-dimensional Motion

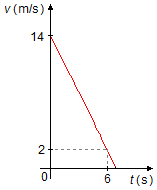
The motion of a particle is described by the velocity-time graph, as shown in the figure. Find:
a) The acceleration of the particle;
b) Write the equation of the speed as a function of time;
c) What is the displacement between 3 s and 7 s?

Solution

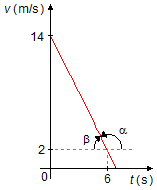
a) Taking two points of the graph, (x₁, y₁) = (6, 2) and (x₂, y₂) = (0, 14). The acceleration of the particle in a velocity-time graph (v × t), will be given by the tangent of the line (Figure 1)

\[ \begin{gather} \bbox[#99CCFF,10px] {a=\tan\alpha =-\tan\beta=\frac{\text{opposite side}}{\text{adjacent side}}=\frac{v_2-v_1}{t_2-t_1}} \end{gather} \]

\[ \begin{gather} a=\frac{14\;\mathrm{\frac{m}{s}}-2\;\mathrm{\frac{m}{s}}}{0-6\;\mathrm s}\\[5pt] a=\frac{12\;\mathrm{\frac{m}{\cancel s}}}{-6\;\mathrm{\cancel s}} \end{gather} \]

Figure 1

\[ \begin{gather} \bbox[#FFCCCC,10px] {a=-2\;\mathrm{m/s^2}} \end{gather} \]

b) The straight line represents the graph of a Linear Equation of the type \( y=ax+b \), comparing with the function for the speed we can make the following associations

\[ \begin{array}{c} y & = & b & + & a x\\ \downarrow & & \downarrow & & \downarrow & \\ v & = & v_0 & + & a t \end{array} \]

the constant a was obtained in the previous item, it corresponds to acceleration a = −2 m/s², and the value of b corresponds to the initial speed of the particle, read in the graph, where the line intercepts the y-axis v₀ = 14 m, the equation of speed as a function of time is

\[ \begin{gather} \bbox[#FFCCCC,10px] {v=14-2t} \end{gather} \]

c) First, we must find the speed of the particle in the instants 3 and 7 seconds using the equation for the speed obtained in the previous item

For t = 3 s

\[ \begin{gather} v(3)=14\;\mathrm{\small{\frac{m}{s}}}-\left(2\;\mathrm{\small{\frac{m}{s^{\cancel 2}}}}\right)(3\;\mathrm{\cancel s})\\[5pt] v(3)=14\;\mathrm{\small{\frac{m}{s}}}-6\;\mathrm{\small{\frac{m}{s}}}\\[5pt] v(3)=8\;\mathrm{m/s} \end{gather} \]

For t = 7 s

\[ \begin{gather} v(7)=14\;\mathrm{\small{\frac{m}{s}}}-\left(2\;\mathrm{\small{\frac{m}{s^{\cancel 2}}}}\right)(7\;\mathrm{\cancel s})\\[5pt] v(7)=14\;\mathrm{\small{\frac{m}{s}}}-14\;\mathrm{\small{\frac{m}{s}}}\\[5pt] v(7)=0 \end{gather} \]

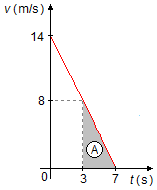
In a graph of velocity versus time v × t, the displacement is numerically equal to the area under the straight line (figure 2), the area of a triangle is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {A=\frac{Bh}{2}} \end{gather} \]

then the displacement will be

\[ \begin{gather} \Delta S\;\overset{\text{N}}{=}\;A=\frac{(7-3)\times 8}{2}\\[5pt] \Delta S=4\times 4 \end{gather} \]

Figure 2

\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta S=16\;\mathrm{m/s}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .