Exercício Resolvido de Movimento Unidimensional
publicidade
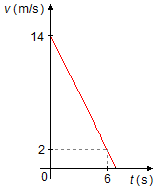
O movimento de um corpo é descrito pelo gráfico da velocidade em função do tempo como mostrado na
figura. Determine:
a) A aceleração do corpo;
b) Escrever a equação horária da velocidade;
c) Qual o espaço percorrido entre 3 s e 7 s?
a) A aceleração do corpo;
b) Escrever a equação horária da velocidade;
c) Qual o espaço percorrido entre 3 s e 7 s?
Solução
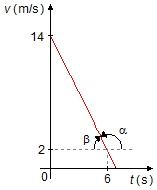
a) Tomamos dois pontos do gráfico, (x1, y1) = (6, 2) e
(x2, y2) = (0, 14). A aceleração do corpo, em um gráfico da
velocidade em função do tempo (v × t), será dada pela tangente da reta (Figura 1)
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a=\operatorname{tg}\alpha =-\operatorname{tg}\beta=\frac{\text{cateto oposto}}{\text{cateto adjacente}}=\frac{v_2-v_1}{t_2-t_1}}
\end{gather}
\]
\[
\begin{gather}
a=\frac{14-2}{0-6}\\[5pt]
a=\frac{12}{-6}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a=-2\;\mathrm{m/s^2}}
\end{gather}
\]
b) A reta representa o gráfico de uma Função de 1.° Grau do tipo \( y=ax+b \), comparando com a função para a velocidade do Movimento Retilíneo Uniformemente Variado (M.R.U.V.) podemos fazer as seguintes associações
\[
\begin{array}{c}
y & = & b & + & a x\\
\downarrow & & \downarrow & & \downarrow & \\
v & = & v_0 & + & a t
\end{array}
\]
o coeficiente a foi obtido no item anterior e corresponde a aceleração
a = −2 m/s2 e o valor de b corresponde a velocidade inicial do corpo que é
lida no gráfico onde a reta corta o eixo das ordenadas como sendo v0 = 14 m, a função
horária da velocidade será
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=14-2t}
\end{gather}
\]
c) Em primeiro lugar devemos determinar as velocidades do corpo nos instantes 3 e 7 segundos usando a expressão para a velocidade obtida no item anterior
- Para t = 3 s
\[
\begin{gather}
v(3)=14-2\times 3\\[5pt]
v(3)=14-6\\[5pt]
v(3)=8\;\mathrm{m/s}
\end{gather}
\]
- Para t = 7 s
\[
\begin{gather}
v(7)=14-2\times 7\\[5pt]
v(7)=14-14\\[5pt]
v(7)=0
\end{gather}
\]
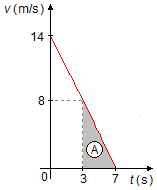
Em um gráfico da velocidade em função do tempo v × t, o espaço percorrido é
numericamente igual a reta sob a curva (Figura 2), a área de um triângulo é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A=\frac{Bh}{2}}
\end{gather}
\]
o espaço percorrido será
\[
\begin{gather}
\Delta S\;\overset{\mathrm{N}}{=}\;A=\frac{(7-3)\times \cancelto{4}{8}}{\cancel 2}\\[5pt]
\Delta S=4\times 4
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta S=16\;\mathrm{m/s}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .