Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
Durante una tormenta, un hombre ve un relámpago, pero escucha el trueno 5 segundos después. La velocidad del sonido en el aire es constante e igual a 340 m/s. Determine:
a) La distancia entre el hombre y el lugar del relámpago;
b) El intervalo de tiempo que la luz tardó en ir desde el lugar del relámpago hasta donde está el hombre. La velocidad de la luz es igual a 300.000 km/s.
Datos del problema:
- Intervalo de tiempo entre el relámpago y el hombre que escucha el trueno: Δt = 5 s;
- Velocidad del sonido en el aire: vs = 340 m/s;
- Velocidad de la luz: c = 300.000 km/s.
El problema se representa con un rayo de luz y una onda de sonido (Figura 1). Como la velocidad de la luz es mucho mayor que la velocidad del sonido, c ≫ vs, el observador ve el relámpago en el mismo instante en que se produce, pero solo escucha el trueno después de un intervalo de tiempo.
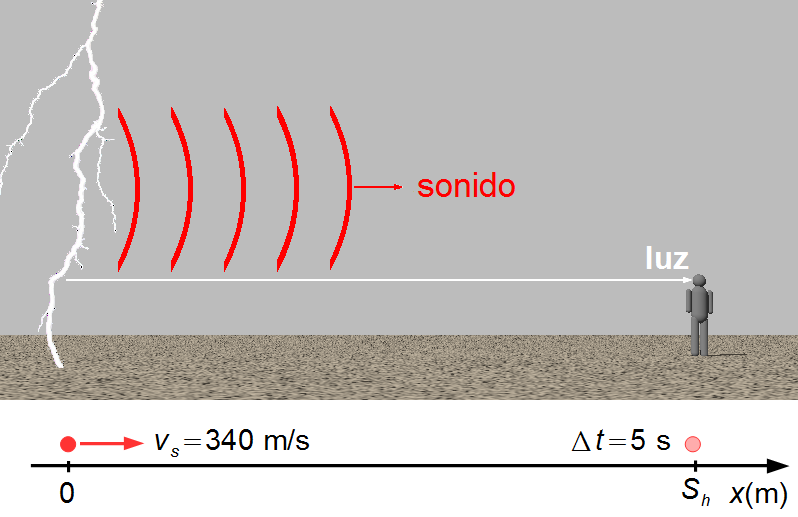
Tomamos un sistema de referencia con origen en donde se produce el relámpago y orientado hacia la derecha donde se encuentra el observador. El problema puede reducirse a un punto material en el origen, S0s = 0, con velocidad constante igual a la velocidad del sonido, vs = 340 m/s, y llegando al observador después de 5 segundos.
Solución
Dado que la onda sonora tiene velocidad constante, está en Movimiento Rectilíneo Uniforme (MRU), dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt} \tag{I}
\end{gather}
\]
\[
\begin{gather}
S_h=S_{0s}+v_s t\\[5pt]
S_h=0+340\times 5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_h=1700\;\mathrm m=1,7\;\mathrm{km}}
\end{gather}
\]
Aplicando la expresión (I) para el rayo de luz, encontramos el intervalo de tiempo para ir desde el punto
donde se produce el relámpago hasta llegar al observador
\[
\begin{gather}
1,7=0+300000t\\[5pt]
t=\frac{1,7}{300000}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t\approx 0,0000057\;\mathrm s=5,7\times 10^{-6}\;\mathrm s}
\end{gather}
\]
Observación: dado que la velocidad de la luz es mucho mayor que la velocidad del sonido, el
intervalo de tiempo que la luz tarda en llegar al observador es muy pequeño. Por lo tanto, podemos suponer
que el observador ve el relámpago en el mismo instante en que se produce y podemos despreciar el intervalo
de tiempo que la luz tarda en llegar al observador en los cálculos.
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .