Solved Problem on One-dimensional Motion

During a thunderstorm, a man sees lightning but hears thunder 5 seconds later. The speed of sound in air is constant and equal to 340 m/s. Determine:
a) The distance between the man and the place of lightning;
b) The time it took for light to go from the location of the lightning to the point where the man is. The speed of light equal to 300,000 km/s.

Problem data:

Time interval between the lightning and the man hearing the thunder: Δt = 5 s;
Speed of sound in air: v_s = 340 m/s;
Speed of light: c = 300.000 km/s.

Problem diagram:

The problem is represented by a ray of light and a wavefront of sound (Figure 1). As the speed of light is much greater than the speed of sound, c ≫ v_s, the observer sees lightning at the same instant it is produced, but only hears thunder after a time interval.

Figure 1

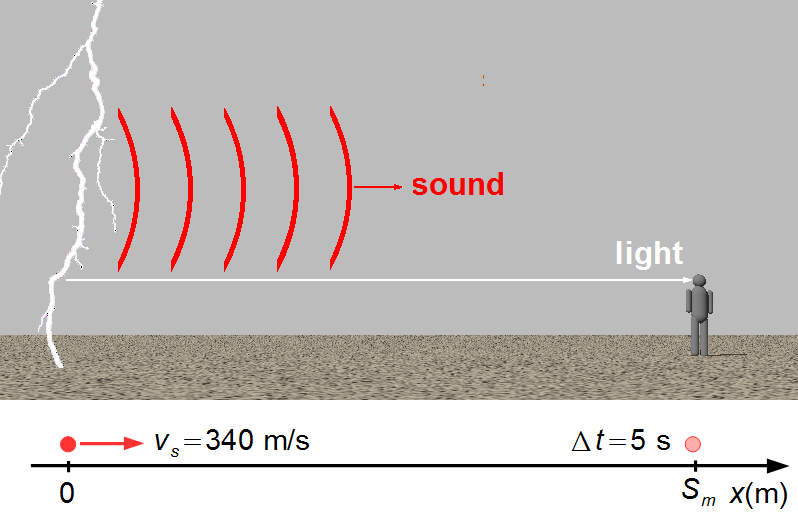
We choose a reference frame with the origin where the lightning is produced and pointing to the right where the observer is. The problem can be reduced to a particle at the origin, S_0s = 0, with a constant speed equal to the speed of sound, v_s = 340 m/s, and arriving at the observer after 5 seconds.

Solution

As the sound wave has a constant speed, the equation of displacement as a function of time is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+vt} \tag{I} \end{gather} \]

\[ \begin{gather} S_m=S_{0s}+v_st\\[5pt] S_m=0+\left(340\;\mathrm{\small{\frac{m}{\cancel s}}}\right)(5\;\mathrm{\cancel s}) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {S_m=1700\;\mathrm m=1.7\;\mathrm{km}} \end{gather} \]

Applying expression (I) to the light ray, we find the time interval to go from the point where the lightning is produced until it reaches the observer

\[ \begin{gather} 1.7\;\mathrm{km}=0+\left(300000\;\mathrm{\small{\frac{km}{s}}}\right)t\\[5pt] t=\frac{1.7\;\mathrm{\cancel{km}}}{300000\;\mathrm{\frac{\cancel{km}}{s}}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {t\approx 0.0000057\;\mathrm s=5.7\times 10^{-6}\;\mathrm s} \end{gather} \]

Note: as the speed of light is much greater than the speed of sound, the time interval that light takes to reach the observer is very small. Therefore, we can assume that the observer sees the lightning at the same instant it is produced, and we can neglect the time interval that the light takes to reach the observer in the calculations.

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .