Pendant un tempête, un homme voit un éclair, mais entend le tonnerre 5 secondes après. La vitesse du son dans l'air est constante et égale à 340 m/s. Déterminer:
a) La distance entre l'homme et le lieu de l'éclair;
b) L'intervalle de temps que la lumière a mis pour aller du lieu de l'éclair jusqu'au point où se trouve l'homme. La vitesse de la lumière est égale à 300 000 km/s.

Données du problème:

• Intervalle de temps entre l'éclair et l'homme entendre le tonnerre:    Δt = 5 s;
• Vitesse du son dans l'air :    v_s = 340 m/s;
• Vitesse de la lumière:    c = 300.000 km/s.

Schéma du problème:

Le problème est représenté par un rayon lumineux et par une onde sonore (Figure 1). Comme la vitesse de la lumière est beaucoup plus grande que la vitesse du son, c ≫ v_s, l'observateur voit l'éclair au moment où il est produit, mais n'entend le tonnerre qu'après un intervalle de temps.


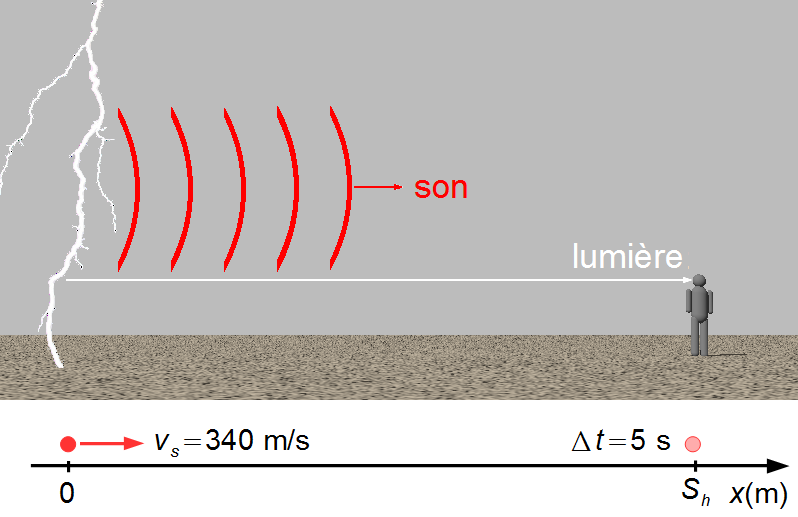
Nous choisissons un référentiel avec l'origine où l'éclair est produit et orienté vers la droite où se trouve l'observateur. Le problème peut être réduit à un point matériel à l'origine, S_0s = 0, avec une vitesse constante égale à la vitesse du son, v_s = 340 m/s, et atteignant l'observateur après 5 secondes.

Solution

Comme l'onde sonore a une vitesse constante, elle est en Mouvement Rectiligne Uniforme donné par En appliquant l'expression (I) pour le rayon lumineux, nous trouvons l'intervalle de temps pour aller du point où l'éclair est produit jusqu'à atteindre l'observateur