Exercício Resolvido de Movimento Unidimensional
publicidade
Durante uma tempestade, um homem vê um relâmpago, mas ouve o trovão 5 segundos depois. Velocidade do som no ar constante e igual a 340 m/s. Determine:
a) A distância entre o homem e o local do relâmpago;
b) O intervalo de tempo que a luz levou para ir do local do relâmpago até o ponto onde o homem está. Velocidade da luz igual a 300.000 km/s.
Dados do problema:
- Intervalo de tempo entre o relâmpago e o homem ouvir o trovão: Δt = 5 s;
- Velocidade do som no ar: vs = 340 m/s;
- Velocidade da luz: c = 300.000 km/s.
O problema é representado por um raio de luz e por uma frente de onda do som (Figura 1). Como a velocidade da luz é muito maior que a velocidade do som, c ≫ vs, o observador vê o relâmpago no mesmo instante em que é produzido, mas só ouve o trovão após um intervalo de tempo.
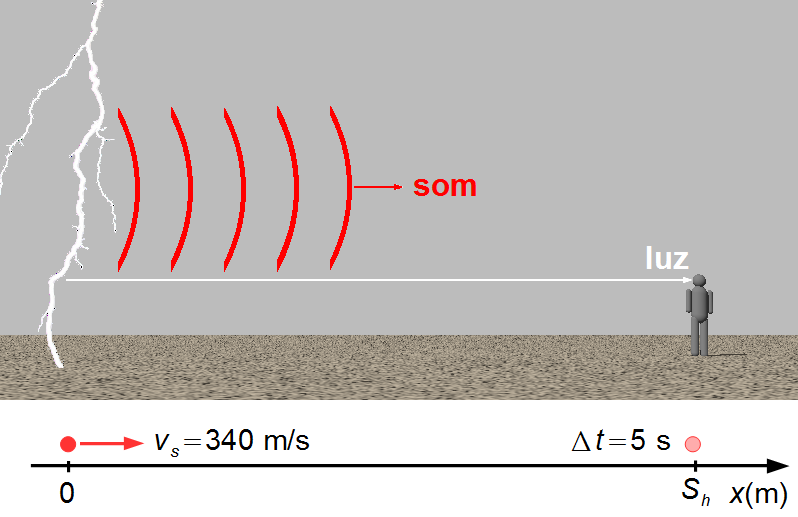
Adotamos um sistema de referência com origem onde o relâmpago é produzido e orientado para a direita onde está o observador. O problema pode ser reduzido a um ponto material na origem, S0s = 0, com velocidade constante igual à velocidade do som, vs = 340 m/s, e chegando observador depois de 5 segundos.
Solução
Como a onda sonora possui velocidade constante ela está em Movimento Retilíneo Uniforme (M.R.U.) dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt} \tag{I}
\end{gather}
\]
\[
\begin{gather}
S_h=S_{0s}+v_s t\\[5pt]
S_h=0+340\times 5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_h=1700\;\mathrm m=1,7\;\mathrm{km}}
\end{gather}
\]
Aplicando a expressão (I) para o raio de luz encontramos o intervalo de tempo para ir do ponto em que o
relâmpago é produzido até chegar ao observador
\[
\begin{gather}
1,7=0+300000t\\[5pt]
t=\frac{1,7}{300000}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t\approx 0,0000057\;\mathrm s=5,7\times 10^{-6}\;\mathrm s}
\end{gather}
\]
Observação: como a velocidade da luz é muito maior que a velocidade do som, o intervalo de
tempo que a luz leva para chegar ao observador é muito pequeno. Por isso podemos admitir que o observador
vê o relâmpago no mesmo instante em que é produzido e podemos desprezar o intervalo de tempo que a luz
leva para chegar ao observador nos cálculos.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .