Ejercicio Resuelto sobre Dinámica
publicidad   



En el sistema de la figura, los cuerpos A y B, con masas de 20 kg y 10 kg respectivamente, están conectados por una cuerda. En la cuerda está fijo un dinamómetro, donde se lee que la fuerza de tensión en la cuerda es de 100 N, y entre el cuerpo A y el plano hay fricción. La cuerda es inextensible y pasa por una polea sin fricción y de masa despreciable. Determinar la aceleración del sistema y el coeficiente de fricción entre el bloque y el plano.


Datos del problema:
  • Masa del cuerpo A:    mA = 20 kg;
  • Masa del cuerpo B:    mB = 10 kg;
  • Lectura de la fuerza de tensión en el dinamómetro:    T = 100 N;
  • Aceleración de la gravedad:    g = 9,8 m/s2.
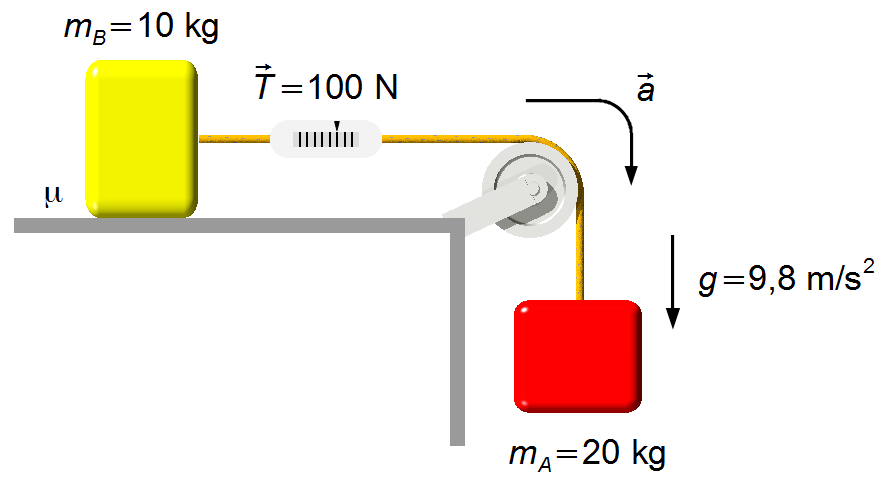
Esquema del problema:

Tomando la aceleración en el sentido en que el cuerpo A está descendiendo, mismo sentido de la aceleración de la gravedad (Figura 1).

Figura 1

Haciendo un Diagrama de Cuerpo Libre tenemos las fuerzas que actúan en los bloques.

  • Bloque A (Figura 2):
    • \( {\vec P}_{\small A} \): peso del bloque A;
    • \( \vec T \): fuerza de tensión en la cuerda.

Figura 2

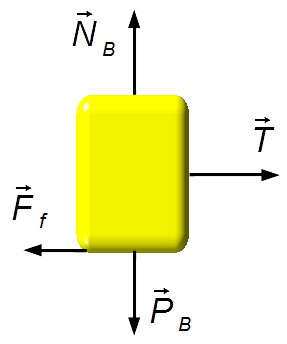
  • Bloque B (Figura 3):
    • Dirección vertical:
      • \( {\vec P}_{\small B} \): peso del cuerpo B;
      • \( {\vec N}_{\small B} \): fuerza de reacción normal de la superficie sobre el cuerpo B.
    • Dirección horizontal:
      • \( \vec T \): fuerza de tensión en la cuerda;
      • \( {\vec F}_{f} \): fuerza de fricción entre el bloque y la superficie.

Figura 3
Solución

Aplicando la Segunda Ley de Newton
\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Bloque A:
\[ \begin{gather} P_{\small A}-T=m_{\small A}a \tag{I} \end{gather} \]
El peso es dado por
\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \tag{II} \end{gather} \]
para el cuerpo A
\[ \begin{gather} P_{\small A}=m_{\small A}g \tag{III} \end{gather} \]
sustituyendo la ecuación (III) en la ecuación (I)
\[ \begin{gather} m_{\small A}g-T=m_{\small A}a\\[5pt] a=\frac{m_{\small A}g-T}{m_{\small A}}\\[5pt] a=\frac{20\times 9,8-100}{20} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a=4,8\;\mathrm{m/s^2}} \end{gather} \]
  • Bloque B:
    • Dirección horizontal:
Aplicando la Segunda Ley de Newton
\[ \begin{gather} T-F_{f}=m_{\small B}a \tag{IV} \end{gather} \]
La fuerza de fricción se da por
\[ \begin{gather} \bbox[#99CCFF,10px] {{\vec F}_{f}=\mu \vec N} \end{gather} \]
para el bloque B
\[ \begin{gather} F_{f}=\mu N_{\small B} \tag{V} \end{gather} \]
sustituyendo la ecuación (V) en la ecuación (IV)
\[ \begin{gather} T-\mu N_{\small B}=m_{\small B}a \tag{VI} \end{gather} \]
  • Bloque B:
    • Dirección vertical:
En esta dirección no hay movimiento, el peso y la reacción normal se equilibran
\[ \begin{gather} N_{\small B}=P_{\small B} \tag{VII} \end{gather} \]
sustituyendo la ecuación (II) para el peso del cuerpo B
\[ \begin{gather} P_{\small B}=m_{\small B}g \tag{VIII} \end{gather} \]
sustituyendo la ecuación (VIII) en la ecuación (VII)
\[ \begin{gather} N_{\small B}=m_{\small B}g \tag{IX} \end{gather} \]
sustituyendo la ecuación (IX) en la ecuación (VI), los datos del problema y la aceleración encontrada arriba
\[ \begin{gather} T-\mu m_{\small B}g=m_{\small B}a\\[5pt] \mu=\frac{T-m_{\small B}a}{m_{\small B}g}\\[5pt] \mu=\frac{100-10\times 4,8}{10\times 9,8} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {\mu\approx 0,5} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .