Solved Problem on Dynamics

In the system of the figure bodies, A and B have masses of 20 kg and 10 kg. respectively. They are tied by a rope, and on the rope is fixed a spring scale, which reads that the force of tension on the cord is 100 N. Between the body A and the plane exists friction. The rope is inextensible and passes through a frictionless pulley and has negligible mass. Determine the acceleration of the system and the coefficient of friction between the block and the plane.

Problem data:

Mass of body A: m_A = 20 kg;
Mass of body B: m_B = 10 kg;
Force in the spring scale: T = 100 N;
Acceleration due to gravity: g = 9.8 m/s².

Problem diagram:

We choose acceleration in the direction that body A is descending, the same direction as the acceleration due to gravity (Figure 1).

Figure 1

Drawing a Free-Body Diagram, we have the forces that act in each of them.

Block A (Figure 2):
- \( {\vec W}_{\small A} \): weight of block A;
- \( \vec T \): tension force on the rope.

Figure 2

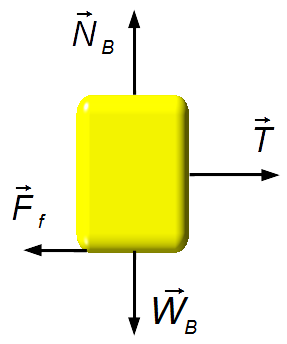
Block B (Figure 3):
- Vertical direction:
  - \( {\vec W}_{\small B} \): weight of block B;
  - \( {\vec N}_{\small B} \): normal reaction force, surface reaction on block B.
- Horizontal direction:
  - \( \vec T \): force of tension on the rope;
  - \( {\vec F}_f \): force of friction between the block and the surface.

Figure 3

Solution

Using Newton's Second Law

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]

Block A:

\[ \begin{gather} W_{\small A}-T=m_{\small A}a \tag{I} \end{gather} \]

The weight is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {W=mg} \tag{II} \end{gather} \]

for the body A

\[ \begin{gather} W_{\small A}=m_{\small A}g \tag{III} \end{gather} \]

substituting equation (III) into equation (I)

\[ \begin{gather} m_{\small A}g-T=m_{\small A}a\\[5pt] a=\frac{m_{\small A}g-T}{m_{\small A}}\\[5pt] a=\frac{(20\;\mathrm{kg})\times\left(9.8\;\mathrm{m/s^2}\right)-(100\;\mathrm N)}{20\;\mathrm{kg}}\\[5pt] a=\frac{96\;\mathrm{\frac{\cancel{kg}.m}{s^2}}}{20\;\mathrm{\cancel{kg}}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {a=4.8\;\mathrm{m/s^2}} \end{gather} \]

Block B:
- Horizontal direction:

Applying the expression (I)

\[ \begin{gather} T-F_f=m_{\small B}a \tag{IV} \end{gather} \]

The force of friction is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {{\vec F}_f=\mu \vec N} \end{gather} \]

for the block B

\[ \begin{gather} F_f=\mu N_{\small B} \tag{V} \end{gather} \]

substituting the equation (V) into equation (IV)

\[ \begin{gather} T-\mu N_{\small B}=m_{\small B}a \tag{VI} \end{gather} \]

Block B:

In this direction, there is no motion, weight, and normal force cancel each other

\[ \begin{gather} N_{\small B}=W_{\small B} \tag{VII} \end{gather} \]

substituting the equation (II) to the weight of body B

\[ \begin{gather} W_{\small B}=m_{\small B}g \tag{VIII} \end{gather} \]

substituting the equation (IX) into equation (VIII)

\[ \begin{gather} N_{\small B}=m_{\small B}g \tag{XI} \end{gather} \]

substituting equation (IX) into equation (VI), the problem data and acceleration found above

\[ \begin{gather} T-\mu m_{\small B}g=m_{\small B}a\\[5pt] \mu=\frac{T-m_{\small B}a}{m_{\small B}g}\\[5pt] \mu=\frac{(100\;\mathrm N)-(10\;\mathrm{kg})\times\left(4.8\;\mathrm{m/s^2}\right)}{(10\;\mathrm{kg})\times\left(9.8\;\mathrm{m/s^2}\right)}\\[5pt] \mu=\frac{52\;\mathrm{\frac{\cancel{kg}.\cancel m}{\cancel{s^2}}}}{98\;\mathrm{\frac{\cancel{kg}.\cancel m}{\cancel{s^2}}}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\mu\approx 0.5} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .