Solved Problem on One-dimensional Motion

An object is launched vertically from the top of a building, passing in front of a window 1.50 m high in 0.09 s. The top of the window is at a distance of 13.00 m from the top of the building. What is the initial velocity of the object?

Problem data:

Height of the window: h = 1.50 m;
Time interval for the object to pass by the window: t = 0.09 s;
Distance from the top of the window to the top of the building: H= 13.00 m;
Acceleration due to gravity: g = 9.80 m/s².

Problem diagram:

We assume that the object is launched with an initial velocity \( {\vec v}_0 \) from the top of the building under the action of the gravitational acceleration \( \vec g \). The object falls 13 m until it reaches the top of a window 1.5 m high, passing through it in 0.09 s with a velocity \( {\vec v}_{0j} \) (Figure 1-A).

Figure 1

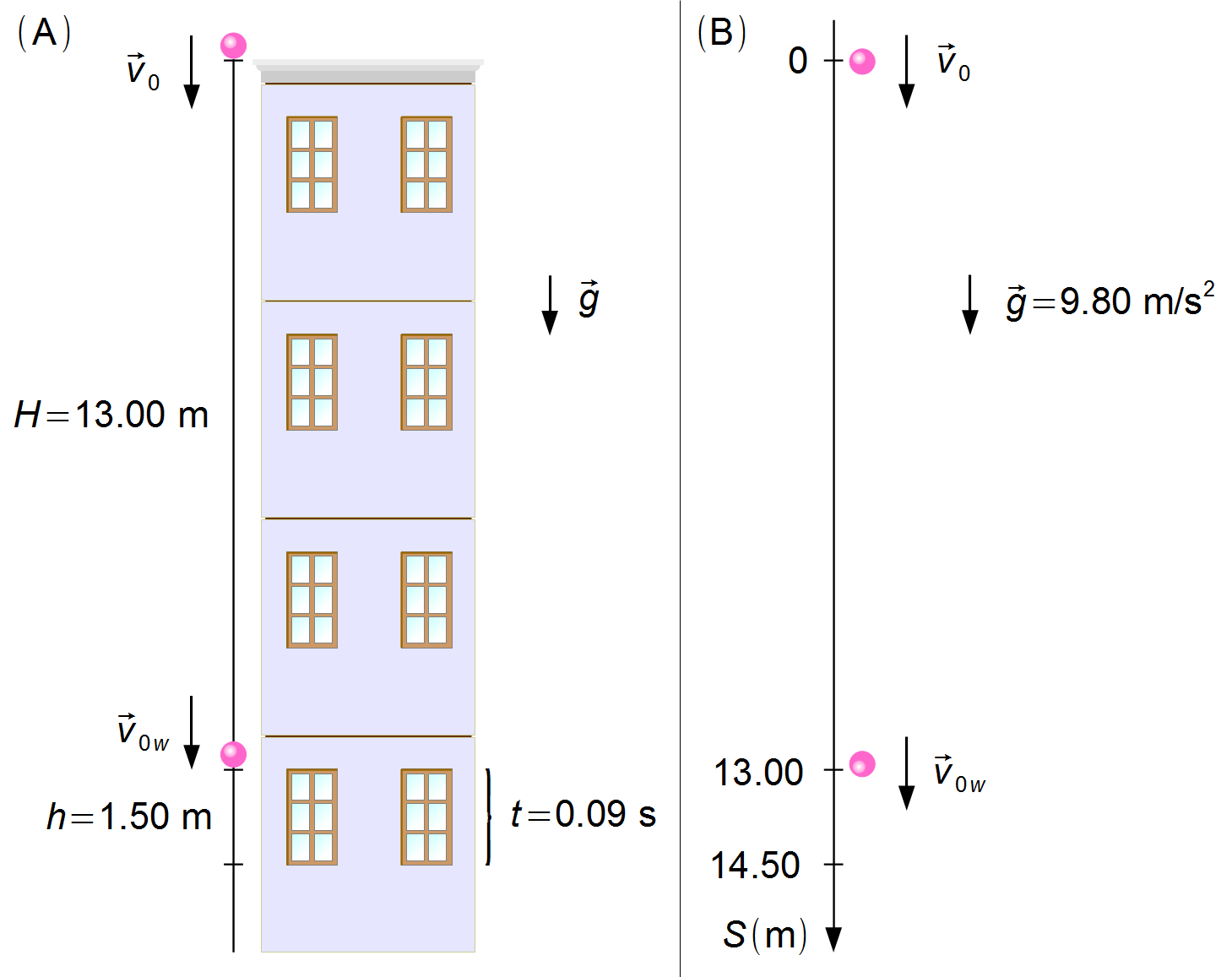
We chose a reference frame with its origin at the top of the building and oriented downward. The acceleration due to gravity and the velocity are in the same direction as the reference frame (Figure 1-B).

Solution

The object starts to pass in front of the window with velocity \( {\vec v}_{0j} \), and the initial position in front of the window is \( S_{0j}=13.00\mathrm m \), the final position is \( S_j=13.00+1.50=14.50\mathrm m \) (Figure 1-B). The object is in free fall given by

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{g}{2}t^2} \end{gather} \]

\[ \begin{gather} S_j=S_{0j}+v_{0j}t+\frac{g}{2}t^2\\[5pt] 14.50\;\mathrm m=13.00\;\mathrm m+v_{0j}\times 0.09\;\mathrm s+\frac{9.80\;\mathrm{\frac{m}{s^2}}}{2}\times(0.09\;\mathrm s)^2\\[5pt] (14.50-13.00)\;\mathrm m=v_{0j}\times0.09\;\mathrm s+0.04\;\mathrm m\\[5pt] v_{0j}=\frac{(1.50-0.04)\;\mathrm m}{0.09\;\mathrm s}\\[5pt] v_{0j}=16.22\;\mathrm{m/s} \end{gather} \]

In the first part of the movement, the initial speed is v₀, which we want to find, the final speed is the speed v_0j found above the initial position is S₀ = 0=0, and the final position is S = 13.00 m. Applying the equation of velocity as a function of acceleration and displacement

\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2g\Delta S} \end{gather} \]

\[ \begin{gather} v_{0j}^2=v_0^2+2g(S-S_0)\\[5pt] \left(16.22\;\mathrm{\small{\frac{m}{s}}}\right)^2=v_0^2+2\times 9.80\;\mathrm{\small{\frac{m}{s^2}}}\times(13.00\;\mathrm m-0)\\[5pt] v_0=\sqrt{(263.09-254.80)\;\mathrm{\small{\frac{m^2}{s^2}}}\;} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {v_0\simeq 2.88\;\mathrm{m/s}} \end{gather} \]

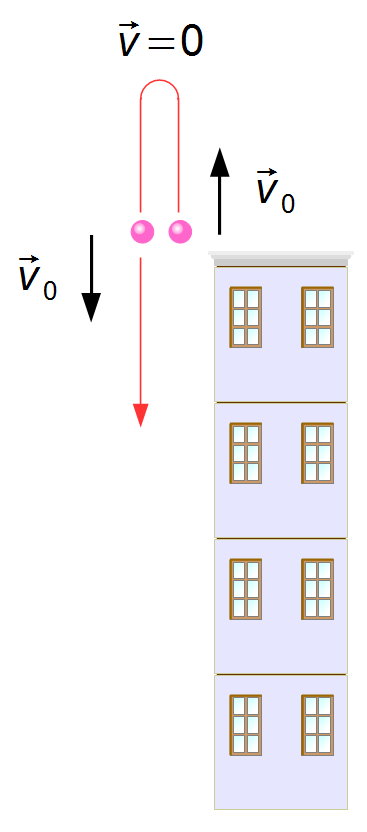
Note: The problem does not state whether the object was launched upwards or downwards, so we randomly assumed it was launched downwards. If the object had been launched upwards with the same initial velocity \( {\vec v}_0 \), it would rise to a height where its velocity would be zero and then start falling. When it passes the top of the building, it would have the same velocity \( {\vec v}_0 \) with which it was initially launched. From then on, the problem would be the same as solved above (Figure 2).

Figure 2

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .