Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
Un objeto es lanzado verticalmente desde la cima de un edificio, pasando frente a una ventana de 1,50 m de altura en 0,09 s. La parte superior de la ventana está a una distancia de 13,00 m de la cima del edificio. ¿Cuál es la velocidad inicial del objeto?
Datos del problema:
- Altura de la ventana: h = 1,50 m;
- Intervalo de tiempo para que el objeto pase por la ventana: t = 0,09 s;
- Distancia de la parte superior de la ventana a la cima del edificio: H= 13,00 m;
- Aceleración de la gravedad: g = 9,80 m/s2.
Vamos a suponer que el objeto es lanzado con una velocidad inicial \( {\vec v}_0 \) desde la cima del edificio bajo la acción de la aceleración de la gravedad \( \vec g \). El objeto cae 13 m hasta alcanzar la parte superior de una ventana de 1,5 m de altura por la que pasa en 0,09 s con una velocidad \( {\vec v}_{0j} \) (Figura 1-A).
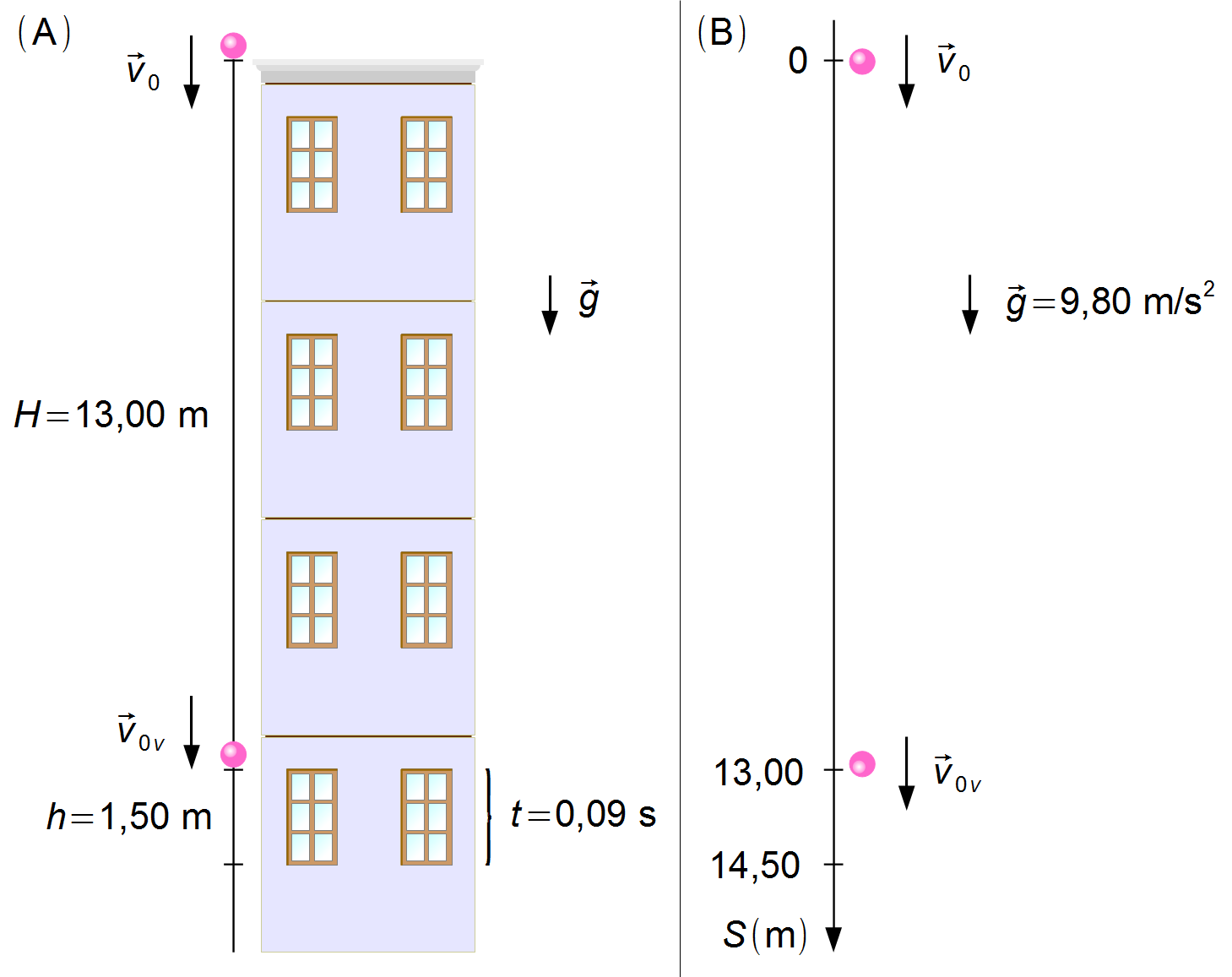
Tomamos un sistema de referencia con origen en la cima del edificio y orientado hacia abajo, la aceleración de la gravedad y la velocidad están en el mismo sentido del referencial (Figura 1-B).
Solución
El objeto comienza a pasar frente a la ventana con una velocidad \( {\vec v}_{0j} \), la posición inicial frente a la ventana es \( S_{0j}=13,00\mathrm m \), la posición final es \( S_j=13,00+1,50=14,50\mathrm m \) (Figura 1-B). El objeto está en caída libre dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{g}{2}t^2}
\end{gather}
\]
\[
\begin{gather}
S_j=S_{0j}+v_{0j}t+\frac{g}{2}t^2\\[5pt]
14,50=13,00+v_{0j}\times 0,09+\frac{9,80}{2}\times 0,09^2\\[5pt]
14,50-13,00=v_{0j}\times0,09+0,04\\[5pt]
v_{0j}=\frac{1,50-0,04}{0,09}\\[5pt]
v_{0j}=16,22\;\mathrm{m/s}
\end{gather}
\]
En la primera parte del movimiento la velocidad inicial es v0, que queremos encontrar, la
velocidad final es la velocidad v0j encontrada arriba, la posición inicial es
S0 = 0 y la posición final es S = 13,00 m. Aplicando la ecuación de la velocidad en
función de la aceleración y el desplazamiento
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v^2=v_0^2+2g\Delta S}
\end{gather}
\]
\[
\begin{gather}
v_{0j}^2=v_0^2+2g(S-S_0)\\[5pt]
16,22^2=v_0^2+2\times 9,80\times (13,00-0)\\[5pt]
v_0=\sqrt{263,09-254,80\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_0\simeq 2,88\;\mathrm{m/s}}
\end{gather}
\]
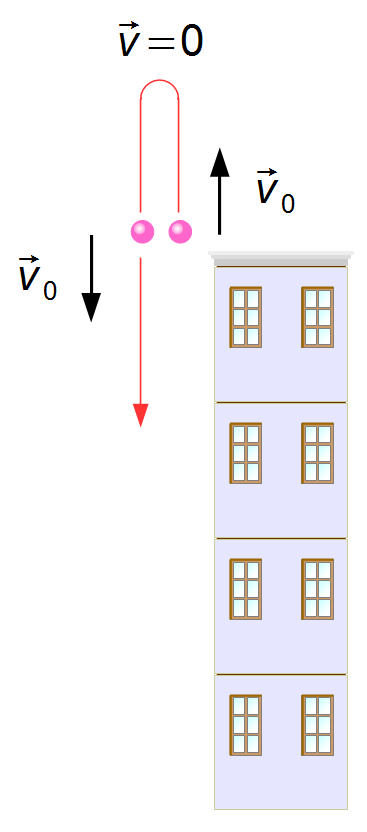
Observación: El problema no dice si el objeto fue lanzado hacia arriba o hacia abajo,
asumimos que fue lanzado hacia abajo aleatoriamente. Si el objeto hubiera sido lanzado hacia arriba con
la misma velocidad inicial
\( {\vec v}_0 \),
subiría hasta una altura donde su velocidad sería igual a cero y comenzaría a caer. En el instante en
que pasara por la cima del edificio tendría la misma velocidad
\( {\vec v}_0 \)
con la que fue lanzado inicialmente, de ahí en adelante el problema sería el mismo resuelto arriba
(Figura 2).
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .