Exercício Resolvido de Movimento Unidimensional
publicidade
Um objeto é lançado verticalmente a partir do alto de um edifício passando em frente a uma janela de 1,50 m de altura em 0,09 s. A parte superior da janela está a uma distância de 13,00 m do topo do edifício. Qual a velocidade inicial do objeto?
Dados do problema:
- Altura da janela: h = 1,50 m;
- Intervalo de tempo para o objeto passar pela janela: t = 0,09 s;
- Distância do alto da janela ao alto do edifício: H= 13,00 m;
- Aceleração da gravidade: g = 9,80 m/s2.
Vamos admitir que o objeto é lançado com velocidade inicial \( {\vec v}_0 \) do topo do edifício sob a ação da aceleração da gravidade \( \vec g \). O objeto cai por 13 m até atingir a parte superior de uma janela de 1,5 m de altura por onde passa em 0,09 s com uma velocidade \( {\vec v}_{0j} \) (Figura 1-A).
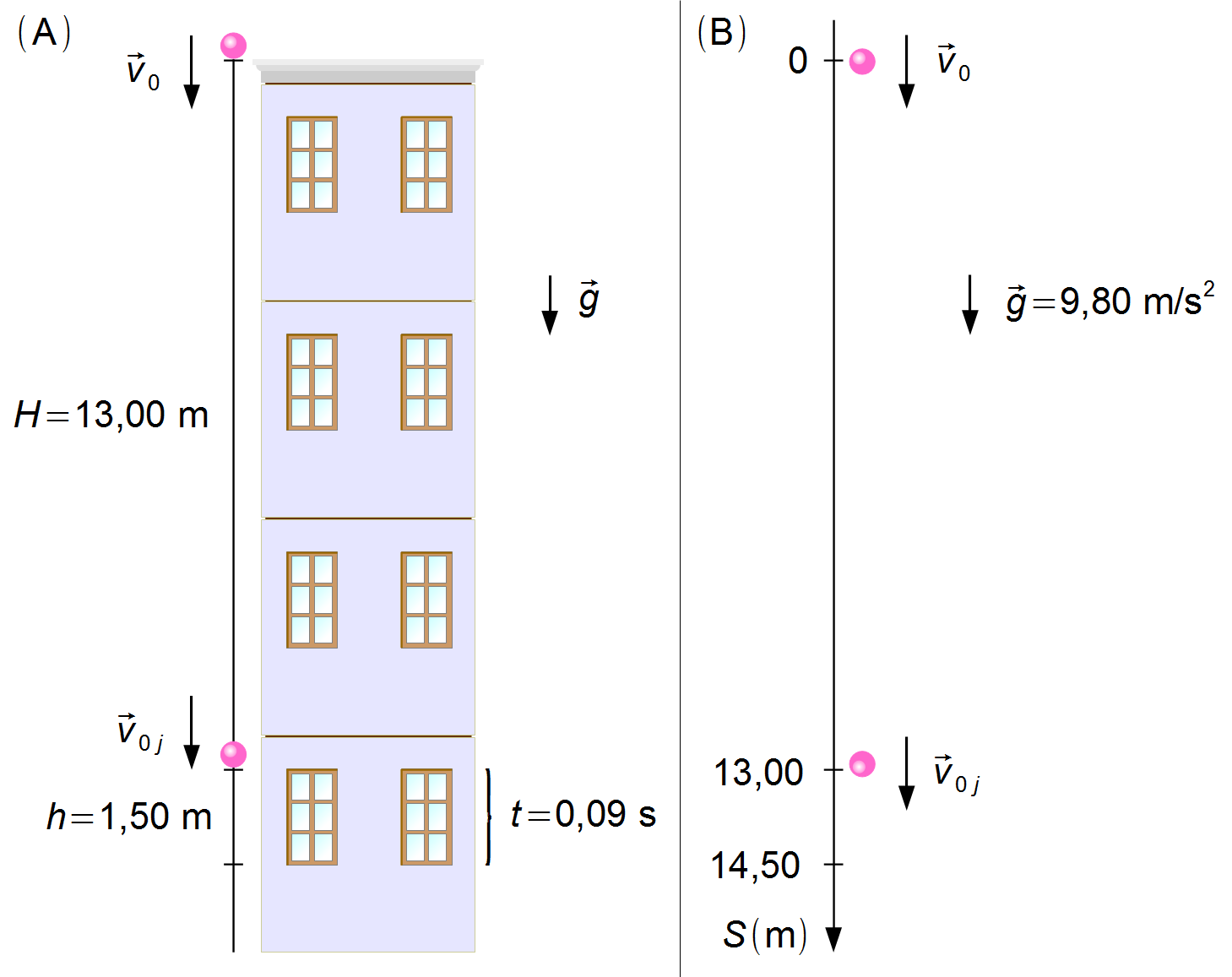
Adotamos um sistema de referência com origem no alto do edifício e orientado para baixo, a aceleração da gravidade e a velocidade estão no mesmo sentido do referencial (Figura 1-B).
Solução
O objeto começa a passar em frente a janela com velocidade \( {\vec v}_{0j} \), a posição inicial em frente da janela é \( S_{0j}=13,00\mathrm m \), a posição final é \( S_j=13,00+1,50=14,50\mathrm m \) (Figura 1-B). O objeto está em queda livre dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{g}{2}t^2}
\end{gather}
\]
\[
\begin{gather}
S_j=S_{0j}+v_{0j}t+\frac{g}{2}t^2\\[5pt]
14,50=13,00+v_{0j}\times 0,09+\frac{9,80}{2}\times 0,09^2\\[5pt]
14,50-13,00=v_{0j}\times0,09+0,04\\[5pt]
v_{0j}=\frac{1,50-0,04}{0,09}\\[5pt]
v_{0j}=16,22\;\mathrm{m/s}
\end{gather}
\]
Na primeira parte do movimento a velocidade inicial é v0, que queremos encontrar, a
velocidade final é a velocidade v0j encontrada acima, a posição inicial é
S0 = 0 e a posição final é S = 13,00 m. Aplicando a Equação de Toriicelli
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v^2=v_0^2+2g\Delta S}
\end{gather}
\]
\[
\begin{gather}
v_{0j}^2=v_0^2+2g(S-S_0)\\[5pt]
16,22^2=v_0^2+2\times 9,80\times (13,00-0)\\[5pt]
v_0=\sqrt{263,09-254,80\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_0\simeq 2,88\;\mathrm{m/s}}
\end{gather}
\]
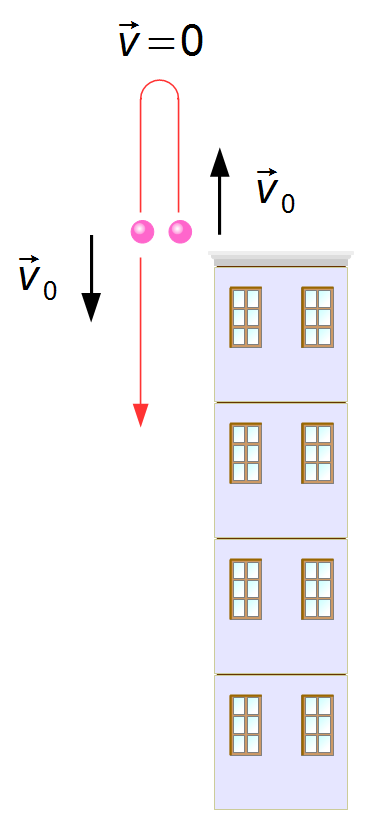
Observação: O problema não diz se o objeto foi lançado para cima ou para baixo, adotamos
que foi para baixo aleatoriamente. Se o objeto tivesse sido lançado para cima com a mesma velocidade
inicial
\( {\vec v}_0 \),
ele subiria até uma altura onde sua velocidade seria igual à zero e começaria a cair. No instante em
que passasse pelo topo do edifício ele teria a mesma velocidade
\( {\vec v}_0 \)
com a qual foi lançada inicialmente, dai em diante o problema seria o mesmo resolvido acima (Figura 2).
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .