Exercice Résolu sur les Mouvement Unidimensionnel

Un objet est lancé verticalement depuis le sommet d'un bâtiment, passant devant une fenêtre de 1,50 m de hauteur en 0,09 s. Le sommet de la fenêtre est à une distance de 13,00 m du sommet du bâtiment. Quelle est la vitesse initiale de l'objet?

Données du problème:

Hauteur de la fenêtre: h = 1,50 m;
Intervalle de temps pour que l'objet passe devant la fenêtre: t = 0,09 s;
Distance du sommet de la fenêtre au sommet du bâtiment: H= 13,00 m;
Accélération de la pesanteur: g = 9,80 m/s².

Schéma du problème:

Nous admettons que l'objet est lancé avec une vitesse initiale \( {\vec v}_0 \) du sommet du bâtiment sous l'action de l'accélération de la pesanteur \( \vec g \). L'objet tombe sur 13 m jusqu'à atteindre le sommet d'une fenêtre de 1,5 m de hauteur où il passe en 0,09 s avec une vitesse \( {\vec v}_{0j} \) (Figure 1-A).

Figure 1

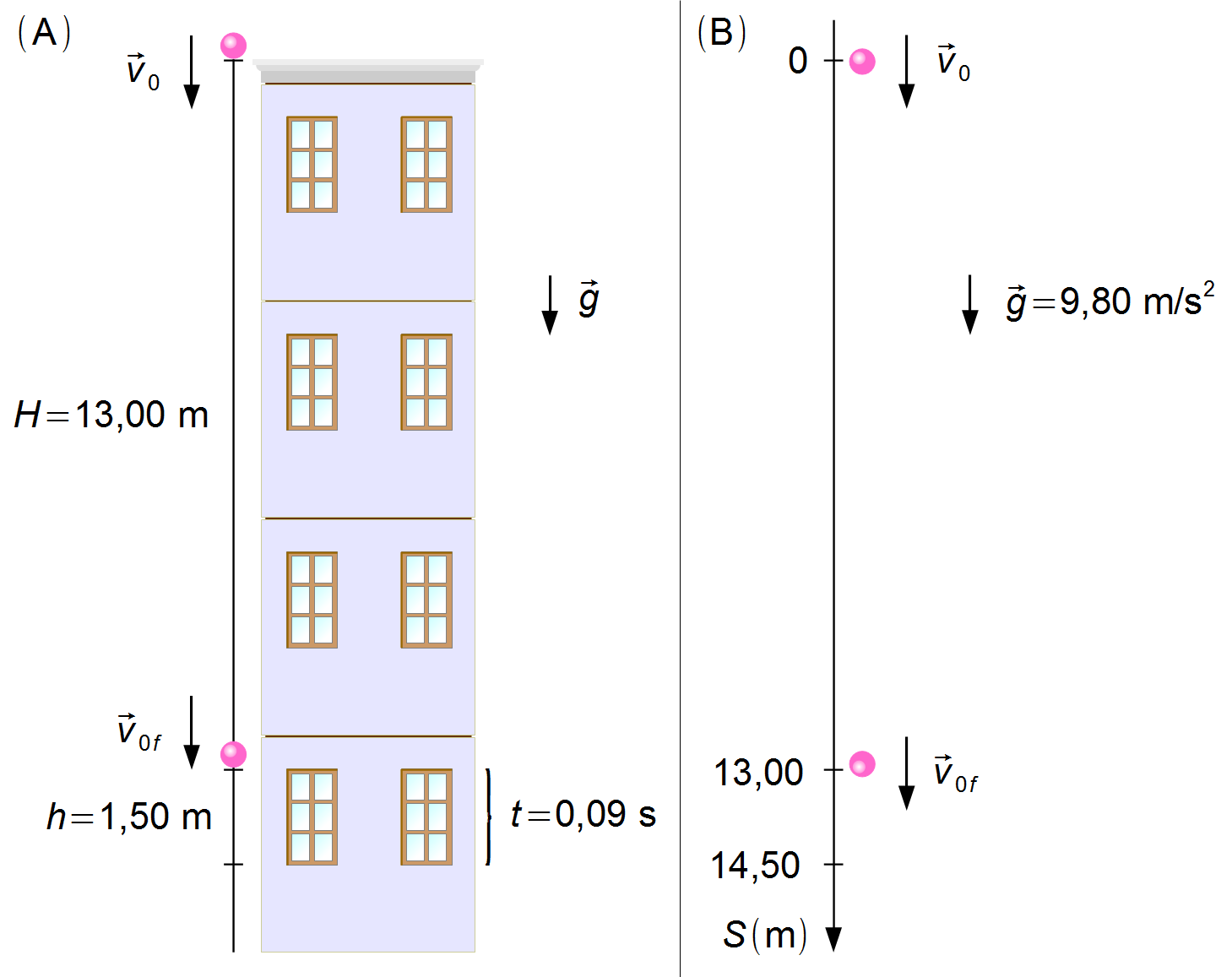
Nous choisissons un référenciel avec une origine au sommet du bâtiment et orienté vers le bas, l'accélération de la pesanteur et la vitesse étant dans le même sens que le référentiel (Figure 1-B).

Solution

L'objet commence à passer devant la fenêtre avec une vitesse \( {\vec v}_{0j} \),, la position initiale devant la fenêtre est \( S_{0j}=13,00\mathrm m \), la position finale est \( S_j=13,00+1,50=14,50\mathrm m \) (Figure 1-B). L'objet est en chute libre donné par

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{g}{2}t^2} \end{gather} \]

\[ \begin{gather} S_j=S_{0j}+v_{0j}t+\frac{g}{2}t^2\\[5pt] 14,50=13,00+v_{0j}\times 0,09+\frac{9,80}{2}\times 0,09^2\\[5pt] 14,50-13,00=v_{0j}\times0,09+0,04\\[5pt] v_{0j}=\frac{1,50-0,04}{0,09}\\[5pt] v_{0j}=16,22\;\mathrm{m/s} \end{gather} \]

Dans la première partie du mouvement, la vitesse initiale est v₀, que nous voulons trouver, la vitesse finale est la vitesse v_0j trouvée ci-dessus, la position initiale est S₀ = 0 et la position finale est S = 13,00 m. En appliquant l'équation de vitesse en fonction de l'accélération et du déplacement

\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2g\Delta S} \end{gather} \]

\[ \begin{gather} v_{0j}^2=v_0^2+2g(S-S_0)\\[5pt] 16,22^2=v_0^2+2\times 9,80\times (13,00-0)\\[5pt] v_0=\sqrt{263,09-254,80\;} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {v_0\simeq 2,88\;\mathrm{m/s}} \end{gather} \]

Remarque: Le problème ne précise pas si l'objet a été lancé vers le haut ou vers le bas, nous avons supposé qu'il était lancé vers le bas de manière aléatoire. Si l'objet avait été lancé vers le haut avec la même vitesse initiale \( {\vec v}_0 \), il monterait jusqu'à une hauteur où sa vitesse serait nulle puis commencerait à tomber. Au moment où il passerait par le sommet du bâtiment, il aurait la même vitesse \( {\vec v}_0 \) avec laquelle il a été lancé initialement. À partir de ce moment, le problème serait le même que celui résolu ci-dessus (Figure 2).

Figure 2

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .