Solved Problem on Circular Motion

A locomotive departs from station A and arrives at station B, 240 km away from station A, after 4 hours. The diameter of the wheels is 1.25 m. Determine:
a) The average number of rotations per minute of each wheel;
b) The angular speed of a point situated on the wheel.

Problem data:

Distance between stations: Δ S = 240 km = 240,000 m;
Time of travel: Δ t = 4 h;
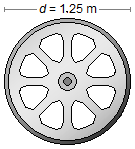
Diameter of a wheel: d = 1.25 m;

Problem diagram:

We chose a reference frame with an origin in station A and pointing to the right towards station B.

Figure 1

Solution

First, we convert the time units, given in hours (h), to minutes (min) used in the problem

\[ \begin{gather} \Delta t=4\;{\mathrm{\cancel h}}\times\frac{60\;\mathrm{{min}}}{1\;\mathrm{{\cancel h}}}=240\;\mathrm{min} \end{gather} \]

Figure 2

a) The number of rotations, n, that the wheel will give throughout the trip will be

\[ \begin{gather} n=\frac{\text{total displacement}}{\text{length of one lap}}=\frac{\Delta S}{C} \tag{I} \end{gather} \]

The length of the circle (one lap) is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {C=2\pi r} \end{gather} \]

as d = 2 r is equal to the diameter of the wheel given in the problem and letting π = 3.14

\[ \begin{gather} C=\pi d\\[5pt] C=3.14\times(1.25\;\mathrm m)\\[5pt] C\approx 3.93\;\mathrm m \end{gather} \]

Substituting this value and the distance traveled given in equation (I)

\[ \begin{gather} n=\frac{240000\;\mathrm m}{3.93\;\mathrm m}\\[5pt] n\approx 61068\;\text{rotations} \tag{II} \end{gather} \]

that is the number of rotations that the wheel makes throughout the trip. Dividing this value by the time of the trip in minutes, found above

\[ \begin{gather} N=\frac{n}{\Delta t}\\[5pt] N=\frac{61068\;\text{rotations}}{240\;\mathrm{min}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {N\approx 254.5\;\mathrm{rpm}} \end{gather} \]

b) The angular velocity is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {\omega=2\pi f} \tag{III} \end{gather} \]

to find the frequency, f, we convert the number of rotations per minute found in the previous item in hertz (Hz)

\[ \begin{gather} f=254.5\;\frac{\text{rotations}}{\cancel{\mathrm{min}}}\times\frac{1\;\mathrm{\cancel{min}}}{60\;\mathrm s}=4.2\;\mathrm{Hz} \end{gather} \]

substituting this value into equation (III)

\[ \begin{gather} \omega=2\times 3.14\times\left(4.2\;\mathrm{\frac{1}{s}}\right) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\omega=26.4\;\mathrm{rad/s}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .