Solved Problem on Circular Motion
advertisement   



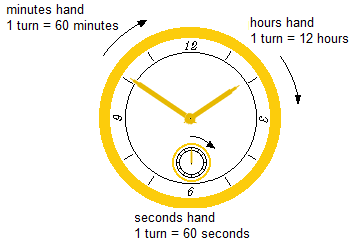
In an old clock of hands, find the period and frequency of rotation of the hours hand, minutes hand, and seconds hand (answers in seconds and hertz).


Problem diagram:

Figure 1

Solution

The hour's hand gives a turn in 12 h. The period will be
\[ \begin{gather} T=\left(12\;\mathrm{\cancel h}\right)\times\left(\frac{3600\;\mathrm s}{1\;\mathrm{\cancel h}}\right) \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {T=43200\;\mathrm s} \end{gather} \]
the frequency as a function of period is given by
\[ \begin{gather} \bbox[#99CCFF,10px] {f=\frac{1}{T}}\tag{I} \end{gather} \]
\[ \begin{gather} f=\frac{1}{43200\;\mathrm s} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {f\approx 0.000023=2.3\times 10^{-5}\;\mathrm{Hz}} \end{gather} \]
The minute's hand gives a turn in 60 min. The period will be
\[ \begin{gather} T=\left(60\;\mathrm{\cancel{min}}\right)\times\left(\frac{60\;\mathrm s}{1\;\mathrm{\cancel{min}}}\right) \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {T=3600\;\mathrm s} \end{gather} \]
for the frequency, applying equation ()
\[ \begin{gather} f=\frac{1}{3600\;\mathrm s} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {f\approx 0.00028=2.8\times 10^{-4}\;\mathrm{Hz}} \end{gather} \]
The second's hand takes a turn in 60 s. The period will be
\[ \begin{gather} \bbox[#FFCCCC,10px] {T=60\;\mathrm s} \end{gather} \]
for the frequency, applying equation (I)
\[ \begin{gather} f=\frac{1}{60\;\mathrm s} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {f\approx 0.017=1.7\times 10^{-2}\;\mathrm{Hz}} \end{gather} \]
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .