Ejercicio Resuelto sobre Movimiento Circular
publicidad
En un reloj tradicional de manecillas, determinar el período y la frecuencia de rotación de las manecillas de las horas, los minutos y los segundos (respuestas en segundos y hertz).
Esquema del problema:
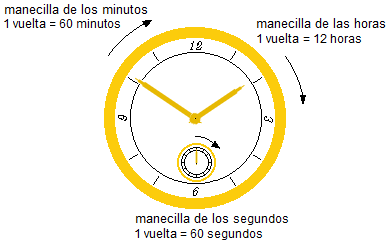
Solución
La manecilla de las horas da una vuelta en 12 horas, su período será
\[
\begin{gather}
T=\left(12\;\mathrm{\cancel h}\right)\times\left(\frac{3600\;\mathrm s}{1\;\mathrm{\cancel h}}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=43200\;\mathrm s}
\end{gather}
\]
la frecuencia en función del período se da por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{f=\frac{1}{T}}\tag{I}
\end{gather}
\]
\[
\begin{gather}
f=\frac{1}{43200\;\mathrm s}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f\approx 0,000023=2,3\times 10^{-5}\;\mathrm{Hz}}
\end{gather}
\]
La manecilla de los minutos da una vuelta en 60 minutos, su período será
\[
\begin{gather}
T=\left(60\;\mathrm{\cancel{min}}\right)\times\left(\frac{60\;\mathrm s}{1\;\mathrm{\cancel{min}}}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=3600\;\mathrm s}
\end{gather}
\]
para la frecuencia, aplicando la ecuación (I)
\[
\begin{gather}
f=\frac{1}{3600\;\mathrm s}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f\approx 0,00028=2,8\times 10^{-4}\;\mathrm{Hz}}
\end{gather}
\]
La manecilla de los segundos da una vuelta en 60 segundos, su período será
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=60\;\mathrm s}
\end{gather}
\]
para la frecuencia, aplicando la ecuación (I)
\[
\begin{gather}
f=\frac{1}{60\;\mathrm s}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f\approx 0,017=1,7\times 10^{-2}\;\mathrm{Hz}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .