Exercício Resolvido de Movimento Circular
publicidade
Em um tradicional relógio de ponteiros determinar o período e a frequência de rotação dos ponteiros das horas, dos minutos e dos segundos (respostas em segundos e hertz).
Esquema do problema:
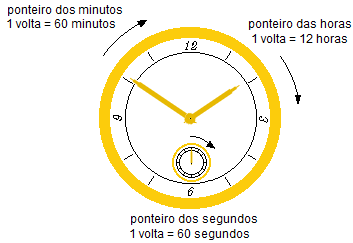
Solução
O ponteiro das horas dá uma volta em 12 h, seu período será
\[
\begin{gather}
T=\left(12\;\mathrm{\cancel h}\right)\times\left(\frac{3600\;\mathrm s}{1\;\mathrm{\cancel h}}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=43200\;\mathrm s}
\end{gather}
\]
a frequência em função do período é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{f=\frac{1}{T}}\tag{I}
\end{gather}
\]
\[
\begin{gather}
f=\frac{1}{43200\;\mathrm s}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f\approx 0,000023=2,3\times 10^{-5}\;\mathrm{Hz}}
\end{gather}
\]
O ponteiro dos minutos dá uma volta em 60 min, seu período será
\[
\begin{gather}
T=\left(60\;\mathrm{\cancel{min}}\right)\times\left(\frac{60\;\mathrm s}{1\;\mathrm{\cancel{min}}}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=3600\;\mathrm s}
\end{gather}
\]
para a frequência, aplicando a equação (I)
\[
\begin{gather}
f=\frac{1}{3600\;\mathrm s}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f\approx 0,00028=2,8\times 10^{-4}\;\mathrm{Hz}}
\end{gather}
\]
O ponteiro dos segundos dá uma volta em 60 s, seu período será
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=60\;\mathrm s}
\end{gather}
\]
para a frequência, aplicando a equação (I)
\[
\begin{gather}
f=\frac{1}{60\;\mathrm s}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f\approx 0,017=1,7\times 10^{-2}\;\mathrm{Hz}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .