Exercice Résolu sur les Mouvement Circulaire
publicité
Dans une horloge traditionnelle à aiguilles, déterminer la période et la fréquence de rotation des aiguilles des heures, des minutes et des secondes (réponses en secondes et hertz).
Schéma du problème
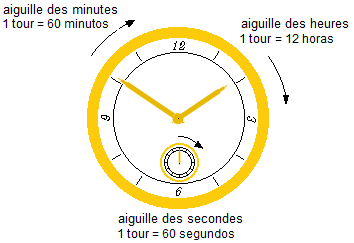
Solution
L'aiguille des heures fait un tour en 12 heures, donc son période sera
\[
\begin{gather}
T=\left(12\;\mathrm{\cancel h}\right)\times\left(\frac{3600\;\mathrm s}{1\;\mathrm{\cancel h}}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=43200\;\mathrm s}
\end{gather}
\]
la fréquence en fonction de la période est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{f=\frac{1}{T}}\tag{I}
\end{gather}
\]
\[
\begin{gather}
f=\frac{1}{43200\;\mathrm s}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f\approx 0,000023=2,3\times 10^{-5}\;\mathrm{Hz}}
\end{gather}
\]
L'aiguille des minutes fait un tour en 60 minutes, donc son période sera
\[
\begin{gather}
T=\left(60\;\mathrm{\cancel{min}}\right)\times\left(\frac{60\;\mathrm s}{1\;\mathrm{\cancel{min}}}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=3600\;\mathrm s}
\end{gather}
\]
pour la fréquence, en appliquant l'équation (I)
\[
\begin{gather}
f=\frac{1}{3600\;\mathrm s}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f\approx 0,00028=2,8\times 10^{-4}\;\mathrm{Hz}}
\end{gather}
\]
L'aiguille des secondes fait un tour en 60 secondes, donc son période sera
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=60\;\mathrm s}
\end{gather}
\]
pour la fréquence, en appliquant l'équation (I)
\[
\begin{gather}
f=\frac{1}{60\;\mathrm s}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f\approx 0,017=1,7\times 10^{-2}\;\mathrm{Hz}}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .