Eine elektrisch geladene Kugel A mit einer Anfangsladung von 8 Coulomb wird mit einer anderen Kugel B in Kontakt gebracht, die eine Ladung von −2 Coulomb besitzt. Nach dem Trennen wird Kugel B mit der Erde verbunden. Anschließend wird eine weitere Kugel C mit einer Anfangsladung von −5 Coulomb mit Kugel A in Kontakt gebracht und danach wieder getrennt. Schließlich wird Kugel A erneut mit Kugel B in Kontakt gebracht und wieder getrennt. Gesucht sind die Endladungen jeder Kugel. Es wird angenommen, dass die drei Kugeln gleich groß sind und aus dem gleichen Material bestehen.

 

Gegebene Daten:

• Ladung der Kugel A:    Q_a = 8 C;
• Ladung der Kugel B:    Q_b = −2 C;
• Ladung der Kugel C:    Q_c = −5 C.

Lösung:

Anfangs haben wir folgende Situation

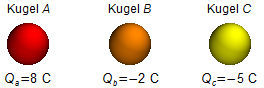
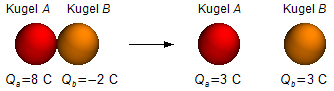
Wenn die Kugeln A und B miteinander in Kontakt gebracht werden, verteilt sich die Gesamtladung gleichmäßig auf beide Kugeln. Die Endladung jeder Kugel entspricht dem Mittelwert der beiden Anfangsladungen.

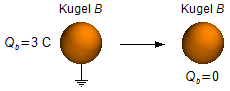
Wird Kugel B mit der Erde verbunden., so entlädt sie sich vollständig, und ihre Ladung wird null.

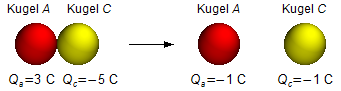
Wenn nun die Kugeln A und C in Kontakt gebracht werden, verteilt sich die Gesamtladung wiederum gleichmäßig auf beide Kugeln. Die Endladung jeder Kugel ist der Mittelwert der Ladungen vor dem Kontakt. Die Ladung von Kugel A ist dabei die zuvor nach dem Kontakt mit B erworbene Ladung ( \( Q_a=3\;\mathrm C \) )

Wenn schließlich die Kugeln A und B erneut in Kontakt gebracht werden, verteilt sich die Gesamtladung wieder gleichmäßig. Für Kugel A verwenden wir den Wert nach dem Kontakt mit C ( \( Q_a=-1\;\mathrm C \) ), und für Kugel B den Wert nach dem Erden ( \( Q_a=-1\;\mathrm C \) ).

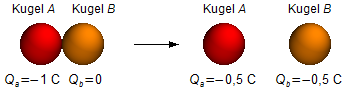
Die Endladungen sind:

• Ladung der Kugel A:  Q_a = − 0,5 C;
  
• Ladung der Kugel B:  Q_b = − 0,5 C;
  
• Ladung der Kugel C:  Q_c = − 1 C.