Exercice Résolu sur les Statique

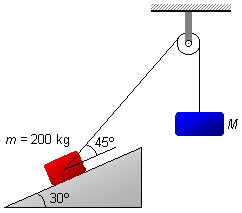
Un corps, de masse 200 kg, est maintenu en équilibre sur un plan incliné à 30° par rapport à l'horizontale à l'aide d'une corde qui passe par une poulie fixe et qui soutient à l'autre extrémité un corps de masse M. La corde forme un angle de 45° avec la ligne inclinée du plan. Déterminer:
a) La masse M;
b) La force exercée par le corps contre le plan.

Données du problème:

Masse du corps sur le plan incliné: m=200 kg;
Angle du plan incliné avec l'horizontale: 30°;
Angle de la corde avec le plan incliné: 45°;
Accélération de la pesanteur: g=9,8 m/s².

Schéma du problème:

En faisant un Diagramme de Corps Libre, nous avons les forces agissant sur les blocs.

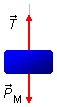
Corps de masse M (Figura 1):
- \( \vec T \): force de tension dans la corde;
- \( {\vec P}_M \): poids du corps suspendu.

Figure 1

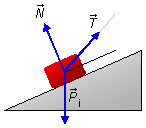
Corps de masse 200 kg (Figura 2):
- \( \vec T \): force de tension dans la corde;
- \( {\vec P}_i \): poids du corps sur le plan incliné;
- \( \vec N \): force normale de réaction du plan sur le bloc.

Figure 2

Solution:

Comme le système est en équilibre, la résultante des forces qui agissent sur lui est égale à zéro

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum \vec F=0} \tag{I} \end{gather} \]

Corps de masse M (Figure 1):

Dans la direction horizontale, il n'y a pas de forces agissant. Dans la direction verticale, le poids \( {\vec P}_M \) et la force de tension \( \vec T \) s'annulent, en appliquant la condition (I)

\[ \begin{gather} T-P_M=0 \tag{II} \end{gather} \]

Corps de masse 200 kg:

Pour le bloc sur le plan incliné, nous choisissons un référentiel xy avec l'axe x dans la direction du plan incliné pointant vers le haut et l'axe y dans la direction perpendiculaire au plan incliné (Figure 3 à gauche).
Dans le triangle ΔAQM, le côté \( \overline{QM} \) est représenté pour le poids \( \vec P \). Nous devons trouver l'angle que fait le poids avec les directions perpendiculaire y et parallèle x au plan incliné.
L'angle \( Q\hat AM \) est donné dans le problème comme étant égal à 30°, le segment \( \overline{QM} \) (la direction où se trouve le poids) est perpendiculaire au segment \( \overline{AC} \). Comme la somme des angles internes d'un triangle est égale à 180°, alors l'angle \( A\hat QM \) doit être

\[ \begin{gather} A\hat QM+30°+90°=180° \\[5pt] A\hat QM=180°-30°-90° \\[5pt] A\hat QM=60° \end{gather} \]

Figure 3

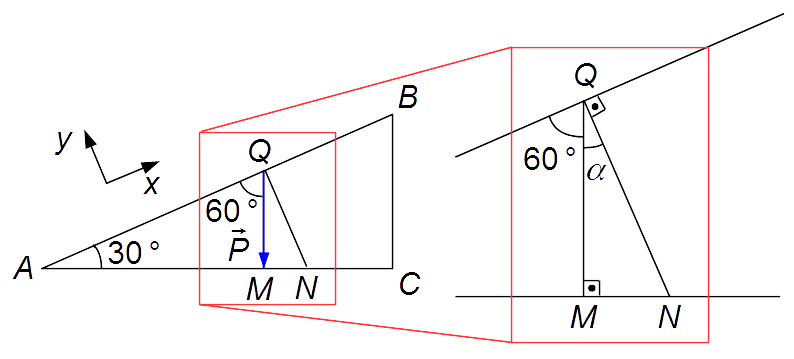
Pour déterminer la valeur de l'angle α (Figure 3 à droite, agrandie), l'angle \( A\hat QM \) vaut 60° et le segment \( \overline{QN} \) est perpendiculaire au segment \( \overline{AB} \), formant un angle de 90°. La somme de ces angles avec l'angle α doit être égale à 180°.

\[ \begin{gather} 60°+90°+\alpha=180° \\[5pt] \alpha=180°-60°-90° \\[5pt] \alpha=30° \end{gather} \]

En dessinant les forces dans un système des coordonnés xy (Figure 4), nous obtenons leurs composantes le long des directions x et y.

Composantes le long de l'axe x

\( N_x=0 \)
\( T_x=T\cos 45° \)
\( P_{ix}=-P_i\cos 60° \)

En appliquant la condition d'équilibre (I)

\[ \begin{gather} N_x+T\cos 45°-P_i\cos 60°=0 \\[5pt] T\cos 45°-P_i\cos 60°=0 \tag{III} \end{gather} \]

Figure 4

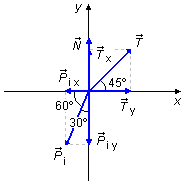
Composantes le long de l'axe y

\( N_y=N \)
\( T_y=T\sin 45° \)
\( P_{iy}=-P_i\sin 60° \)

En appliquant la condition d'équilibre (I)

\[ \begin{gather} N+T\sin 45°-P_i\sin 60°=0 \tag{IV} \end{gather} \]

a) Le poids est donné par

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]

Selon la Trigonométrie

\( \cos 45°=\sin 45°=\dfrac{\sqrt{2\;}}{2} \)
\( \cos 60°=\dfrac{1}{2} \), \( \sin 60°=\dfrac{\sqrt{3\;}}{2} \)

Les équations (II), (III) et (IV) forment un système de trois équations à trois inconnues (N, T et M)

\[ \begin{gather} \left\{ \begin{array}{l} T-Mg=0 \\ \dfrac{\sqrt{2\;}}{2}T-\dfrac{1}{2}mg=0 \\ N+\dfrac{\sqrt{2\;}}{2}T-\dfrac{\sqrt{\;3\;}}{2}mg=0 \tag{V} \end{array} \right. \end{gather} \]

en isolant la valeur de la force de tension, T, dans la première équation du système (V)

\[ \begin{gather} T=Mg \tag{VI} \end{gather} \]

et en la remplaçant dans la deuxième équation du système (V)

\[ \begin{gather} \frac{\sqrt{2\;}}{2}Mg-\frac{1}{2}mg=0 \\[5pt] \frac{\sqrt{2\;}}{\cancel 2}M\cancel g=\frac{1}{\cancel 2}m\cancel g \\[5pt] \sqrt{2\;}M=m \\[5pt] M=\frac{m}{\sqrt{2\;}} \end{gather} \]

en remplaçant la valeur de m donnée dans le problème et \( \sqrt{2\;}\approx 1,4142 \)

\[ \begin{gather} M=\frac{200}{1,4142} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {M=141,4\;\mathrm{kg}} \end{gather} \]

b) La force exercée sur le plan \( F_p \) sera donnée par la composante y de le poids sur le plan incliné

\[ \begin{gather} F_p=P_{iy}=-P_i\sin 60° \\[5pt] F_p=-mg\sin 60° \\[5pt] F_p=-200\times 9,8\times\frac{\sqrt{3\;}}{2} \end{gather} \]

étant donné que \( \sqrt{3\;}\approx 1,7321 \)

\[ \begin{gather} \bbox[#FFCCCC,10px] {F_p=-1697\;\mathrm N} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .