Ejercicio Resuelto sobre Estática

Un cuerpo, de masa 200 kg, se mantiene en equilibrio sobre un plano inclinado de 30° con respecto a la horizontal mediante una cuerda que pasa por una polea fija, y que sostiene en el otro extremo un cuerpo de masa M. La cuerda forma con la línea inclinada del plano un ángulo de 45°. Determinar:
a) La masa M;
b) La fuerza ejercida por el cuerpo contra el plano.

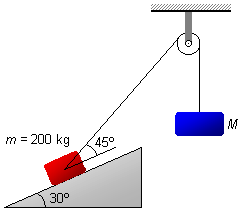
Datos del problema:

Masa del cuerpo en el plano inclinado: m=200 kg;
Ángulo del plano inclinado con la horizontal: 30°;
Ángulo de la cuerda con el plano inclinado: 45°;
Aceleración de la gravedad: g=9,8 m/s².

Esquema del problema:

Aislamos los cuerpos y analizamos las fuerzas que actúan sobre cada uno de ellos.

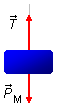
Cuerpo de masa M (Figura 1):
- \( \vec T \): tensión en la cuerda;
- \( {\vec P}_M \): peso del cuerpo suspendido.

Figura 1

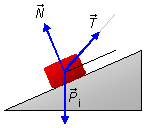
Cuerpo de masa 200 kg (Figura 2):
- \( \vec T \): tensión en la cuerda;
- \( {\vec P}_i \): peso del cuerpo en el plano inclinado;
- \( \vec N \): fuerza normal de reacción del plano sobre el bloque.

Figura 2

Solución:

Como el sistema está en equilibrio, la resultante de las fuerzas que actúan sobre él es igual a cero

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum \vec F=0} \tag{I} \end{gather} \]

Cuerpo de masa M (Figura 1):

En la dirección horizontal no existen fuerzas actuando. En la dirección vertical, el peso \( {\vec P}_M \) y la tensión \( \vec T \) se anulan, aplicando la condición (I)

\[ \begin{gather} T-P_M=0 \tag{II} \end{gather} \]

Cuerpo de masa 200 kg:

Para el bloque sobre el plano inclinado, elegimos un sistema de referencia xy con el eje-x en la dirección del plano inclinado y apuntando hacia arriba, y el eje-y en la dirección perpendicular al plano inclinado (Figura 3 a la izquierda).
En el triángulo ΔAQM, el cateto \( \overline{QM} \) está representado por el peso \( \vec P \). Debemos encontrar el ángulo que forma el peso con las direcciones perpendiculares, y, y paralela, x, al plano inclinado.
El ángulo \( Q\hat AM \) es dado en el problema como 30°, el segmento \( \overline{QM} \) (dirección donde está el peso) es perpendicular al segmento \( \overline{AC} \). Como la suma de los ángulos internos de un triángulo es igual a 180°, entonces el ángulo \( A\hat QM \) debe ser

\[ \begin{gather} A\hat QM+30°+90°=180° \\[5pt] A\hat QM=180°-30°-90° \\[5pt] A\hat QM=60° \end{gather} \]

Figura 3

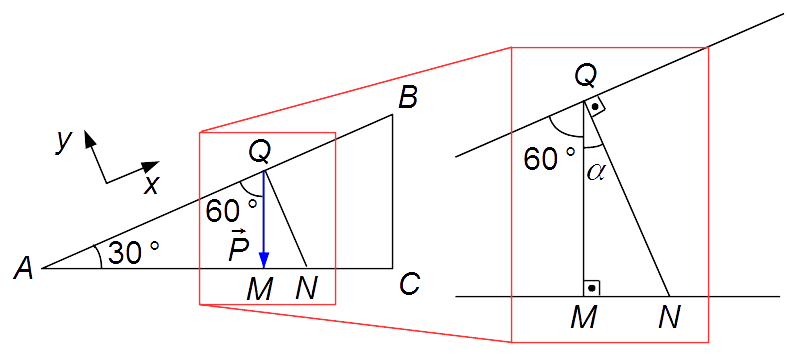
Para determinar el valor del ángulo α (Figura 3 a la derecha, ampliada), el ángulo \( A\hat QM \) vale 60°, y el segmento \( \overline{QN} \) es perpendicular al segmento \( \overline{AB} \), formando un ángulo de 90º, por lo que la suma de estos ángulos con el ángulo α debe ser 180°

\[ \begin{gather} 60°+90°+\alpha=180° \\[5pt] \alpha=180°-60°-90° \\[5pt] \alpha=30° \end{gather} \]

Dibujando las fuerzas en un sistema de coordenadas xy (Figura 4), obtenemos sus componentes a lo largo de las direcciones x e y.

Componentes a lo largo del eje-x

\( N_x=0 \)
\( T_x=T\cos 45° \)
\( P_{ix}=-P_i\cos 60° \)

Aplicando la condición de equilibrio (I)

\[ \begin{gather} N_x+T\cos 45°-P_i\cos 60°=0 \\[5pt] T\cos 45°-P_i\cos 60°=0 \tag{III} \end{gather} \]

Figura 4

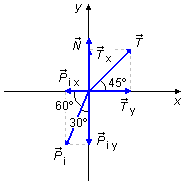
Componentes a lo largo del eje-y

\( N_y=N \)
\( T_y=T\operatorname{sen}45° \)
\( P_{iy}=-P_i\operatorname{sen}60° \)

Aplicando la condición de equilibrio (I)

\[ \begin{gather} N+T\operatorname{sen}45°-P_i\operatorname{sen}60°=0 \tag{IV} \end{gather} \]

a) El peso está dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]

De la Trigonometría

\( \cos 45°=\operatorname{sen}45°=\dfrac{\sqrt{2\;}}{2} \)
\( \cos 60°=\dfrac{1}{2} \), \( \operatorname{sen}60°=\dfrac{\sqrt{3\;}}{2} \)

Las ecuaciones (II), (III) y (IV) forman un sistema de tres ecuaciones con tres incógnitas (N, T y M)

\[ \begin{gather} \left\{ \begin{array}{l} T-Mg=0 \\ \dfrac{\sqrt{2\;}}{2}T-\dfrac{1}{2}mg=0 \\ N+\dfrac{\sqrt{2\;}}{2}T-\dfrac{\sqrt{\;3\;}}{2}mg=0 \tag{V} \end{array} \right. \end{gather} \]

aislando el valor de la tensión, T, en la primera ecuación del sistema (V)

\[ \begin{gather} T=Mg \tag{VI} \end{gather} \]

y sustituyendo en la segunda ecuación del sistema (V)

\[ \begin{gather} \frac{\sqrt{2\;}}{2}Mg-\frac{1}{2}mg=0 \\[5pt] \frac{\sqrt{2\;}}{\cancel 2}M\cancel g=\frac{1}{\cancel 2}m\cancel g \\[5pt] \sqrt{2\;}M=m \\[5pt] M=\frac{m}{\sqrt{2\;}} \end{gather} \]

sustituyendo el valor de m dado en el problema y \( \sqrt{2\;}\approx 1,4142 \)

\[ \begin{gather} M=\frac{200}{1,4142} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {M=141,4\;\mathrm{kg}} \end{gather} \]

b) La fuerza ejercida sobre el plano \( F_p \) será dada por la componente y de la fuerza peso sobre el plano inclinado

\[ \begin{gather} F_p=P_{iy}=-P_i\operatorname{sen}60° \\[5pt] F_p=-mg\operatorname{sen}60° \\[5pt] F_p=-200\times 9,8\times\frac{\sqrt{3\;}}{2} \end{gather} \]

siendo \( \sqrt{3\;}\approx 1,7321 \)

\[ \begin{gather} \bbox[#FFCCCC,10px] {F_p=-1697\;\mathrm N} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .