Exercice Résolu sur les Statique
publicité
Pour le système en équilibre sur la figure, déterminer les tensions dans les cordes A et B
en sachant que le corps C a un poids de 100 N.
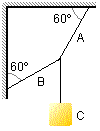
Données du problème
- Poids du corps C: P = 100 N.
Schéma du problème:
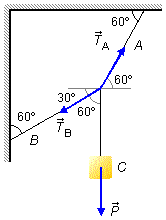
Les forces qui agissent sur le système sont le poids \( \vec P \) du bloc C qui pointe vers le bas et les tensions dans les cordes. La corde qui soutient le bloc transmet simplement le poids du bloc au point où elle est fixée aux autres cordes.
La corde A forme un angle de 60° avec le plafond. En traçant une ligne horizontale qui passe par le point où elle est attachée au corps C, on constate que la force de tension \( {\vec T}_A \) forme également un angle de 60° avec l’horizontale. Ces angles sont alternes internes.
La corde B forme un angle de 60° avec le mur vertical, l'angle entre la force de tension \( {\vec T}_B \) et la corde qui soutient le bloc C est également de 60°, ces angles sont alternes internes. L’angle entre la ligne horizontale et la force de tension \( {\vec T}_B \) est de 30° par rapport à l’horizontale, ce sont des angles complémentaires, leur somme est égale à 90°.
Les forces qui agissent sur le système sont le poids \( \vec P \) du bloc C qui pointe vers le bas et les tensions dans les cordes. La corde qui soutient le bloc transmet simplement le poids du bloc au point où elle est fixée aux autres cordes.
La corde A forme un angle de 60° avec le plafond. En traçant une ligne horizontale qui passe par le point où elle est attachée au corps C, on constate que la force de tension \( {\vec T}_A \) forme également un angle de 60° avec l’horizontale. Ces angles sont alternes internes.
La corde B forme un angle de 60° avec le mur vertical, l'angle entre la force de tension \( {\vec T}_B \) et la corde qui soutient le bloc C est également de 60°, ces angles sont alternes internes. L’angle entre la ligne horizontale et la force de tension \( {\vec T}_B \) est de 30° par rapport à l’horizontale, ce sont des angles complémentaires, leur somme est égale à 90°.
Solution:
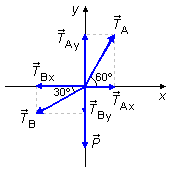
Nous dessinons les forces dans un système de coordonnés xy et décomposons les forces dans ces
directions (Figure 2). Le poids
\( \vec P \)
a uniquement une composante dans la direction y négative. La force de tension
\( {\vec T}_A \)
a une composante
\( {\vec T}_{Ax} \)
dans la direction x positive et une composante
\( {\vec T}_{Ay} \)
dans la direction y positive. La force de tension
\( {\vec T}_B \)
a une composante
\( {\vec T}_{Bx} \)
dans la direction x négative et une composante
\( {\vec T}_{By} \)
dans la direction y négative.
Étant donné que le système est en équilibre, la résultante des forces qui agissent sur lui est égale à zéro
Étant donné que le système est en équilibre, la résultante des forces qui agissent sur lui est égale à zéro
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum \vec{F}=0}
\end{gather}
\]
\[
\begin{gather}
{\vec T}_A+{\vec T}_B+\vec P=0 \\[5pt]
{\vec T}_{Ax}+{\vec T}_{Ay}-{\vec T}_{Bx}-{\vec T}_{By}-\vec P=0 \tag{I}
\end{gather}
\]
- Direction x:
\[
\begin{gather}
{\vec T}_{Ax}=T_A\cos 60° \tag{II}
\end{gather}
\]
\[
\begin{gather}
{\vec T}_{Bx}=T_B\cos 30° \tag{III}
\end{gather}
\]
Le poids n’a pas de composante dans la direction x.
- Direction y:
\[
\begin{gather}
{\vec T}_{Ay}=T_A\operatorname{sen}60° \tag{IV}
\end{gather}
\]
\[
\begin{gather}
{\vec T}_{Bx}=T_B\operatorname{sen}30° \tag{V}
\end{gather}
\]
En substituant les équations (II), (III), (IV) et (V) dans l’équation (I) et en séparant les composantes dans
les directions x et y
- Direction x:
\[
\begin{gather}
T_A\cos 60°-T_B\cos 30°=0
\end{gather}
\]
- Direction y:
\[
\begin{gather}
T_A\operatorname{sen}60°-T_B\operatorname{sen}30°-P=0
\end{gather}
\]
D’après la Trigonométrie
\( \cos 30°=\dfrac{\sqrt{3\;}}{2} \),
\( \sin 30°=\dfrac{1}{2} \),
\( \cos 60°=\dfrac{1}{2} \), \( \operatorname{sen}60°\dfrac{\sqrt{3\;}}{2} \).
\( \cos 60°=\dfrac{1}{2} \), \( \operatorname{sen}60°\dfrac{\sqrt{3\;}}{2} \).
\[
\left\{
\begin{array}{l}
\dfrac{1}{2}T_A-\dfrac{\sqrt{3\;}}{2}T_B=0 \\
\dfrac{\sqrt{3\;}}{2}T_A-\dfrac{1}{2}T_B-100=0
\end{array}
\right.
\]
C'est un système de deux équations à deux inconnues (TA et TB). En
isolant la valeur de TA dans la première équation du système et en substituant dans la
deuxième équation
\[
\begin{gather}
\frac{1}{\cancel 2}T_A=\frac{\sqrt{3\;}}{\cancel 2}T_B\\[5pt]
T_A=\sqrt{3\;}\;T_B \tag{VI}
\end{gather}
\]
\[
\begin{gather}
\frac{\sqrt{3\;}}{2}\times\sqrt{3\;}\;T_B-\frac{1}{2}T_B-100=0 \\[5pt]
\frac{3}{2}T_B-\frac{1}{2}T_B=100 \\[5pt]
\frac{2}{2}T_B=100
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_B=100\;\mathrm N}
\end{gather}
\]
en substituant la valeur trouvée ci-dessus dans l’équation (VI), nous obtenons TA
\[
\begin{gather}
T_A=\sqrt{3\;}\times 100
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_A \approx 173\;\mathrm N}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .