Ejercicio Resuelto sobre Estática
publicidad
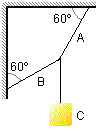
Para el sistema en equilibrio en la figura, determine las tensiones en las cuerdas A y B
sabiendo que el cuerpo C tiene 100 N.
Dado del problema:
- Peso del cuerpo C: P = 100 N.
Esquema del problema:
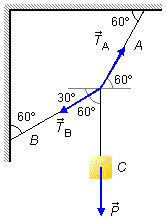
Las fuerzas que actúan en el sistema son el peso \( \vec P \) del bloque C que apunta hacia abajo y las tensiones en las cuerdas. La cuerda que sostiene el bloque solo transmite la fuerza de peso del bloque al punto donde está fijada a las otras cuerdas.
La cuerda A forma un ángulo de 60° con el techo, trazando una línea horizontal que pasa por el punto donde está sujeta al cuerpo C, tenemos que la fuerza de tensión \( {\vec T}_A \) también forma un ángulo de 60° con la horizontal, siendo estos ángulos alternos internos. La cuerda B forma un ángulo de 60° con la pared vertical, el ángulo entre la fuerza de tensión \( {\vec T}_B \) y la cuerda que sostiene el bloque C también es de 60°, siendo estos ángulos alternos internos. El ángulo entre la línea horizontal y la fuerza de tensión \( {\vec T}_B \) es de 30° con la horizontal, son ángulos complementarios, suman 90°.
Las fuerzas que actúan en el sistema son el peso \( \vec P \) del bloque C que apunta hacia abajo y las tensiones en las cuerdas. La cuerda que sostiene el bloque solo transmite la fuerza de peso del bloque al punto donde está fijada a las otras cuerdas.
La cuerda A forma un ángulo de 60° con el techo, trazando una línea horizontal que pasa por el punto donde está sujeta al cuerpo C, tenemos que la fuerza de tensión \( {\vec T}_A \) también forma un ángulo de 60° con la horizontal, siendo estos ángulos alternos internos. La cuerda B forma un ángulo de 60° con la pared vertical, el ángulo entre la fuerza de tensión \( {\vec T}_B \) y la cuerda que sostiene el bloque C también es de 60°, siendo estos ángulos alternos internos. El ángulo entre la línea horizontal y la fuerza de tensión \( {\vec T}_B \) es de 30° con la horizontal, son ángulos complementarios, suman 90°.
Solución:
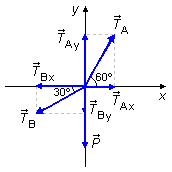
Dibujamos las fuerzas en un sistema de ejes coordenados xy y descomponemos las fuerzas en esas
direcciones (Figura 2). La fuerza de peso
\( \vec P \)
solo tiene el componente en la dirección y negativa. La fuerza de tensión
\( {\vec T}_A \)
tiene el componente
\( {\vec T}_{Ax} \)
en la dirección x positiva y el componente
\( {\vec T}_{Ay} \)
en la dirección y positiva. La fuerza de tensión
\( {\vec T}_B \)
tiene el componente
\( {\vec T}_{Bx} \)
en la dirección x negativa y el componente
\( {\vec T}_{By} \)
en la dirección y negativa.
Como el sistema está en equilibrio, la resultante de las fuerzas que actúan sobre él es igual a cero
Como el sistema está en equilibrio, la resultante de las fuerzas que actúan sobre él es igual a cero
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum \vec{F}=0}
\end{gather}
\]
\[
\begin{gather}
{\vec T}_A+{\vec T}_B+\vec P=0 \\[5pt]
{\vec T}_{Ax}+{\vec T}_{Ay}-{\vec T}_{Bx}-{\vec T}_{By}-\vec P=0 \tag{I}
\end{gather}
\]
- Dirección x:
\[
\begin{gather}
{\vec T}_{Ax}=T_A\cos 60° \tag{II}
\end{gather}
\]
\[
\begin{gather}
{\vec T}_{Bx}=T_B\cos 30° \tag{III}
\end{gather}
\]
La fuerza de peso no tiene componente en la dirección x.
- Dirección y:
\[
\begin{gather}
{\vec T}_{Ay}=T_A\operatorname{sen}60° \tag{IV}
\end{gather}
\]
\[
\begin{gather}
{\vec T}_{Bx}=T_B\operatorname{sen}30° \tag{V}
\end{gather}
\]
Sustituyendo las ecuaciones (II), (III), (IV) y (V) en la ecuación (I) y separando los componentes en las
direcciones x y y
- Dirección x:
\[
\begin{gather}
T_A\cos 60°-T_B\cos 30°=0
\end{gather}
\]
- Dirección y:
\[
\begin{gather}
T_A\operatorname{sen}60°-T_B\operatorname{sen}30°-P=0
\end{gather}
\]
De la Trigonometría
\( \cos 30°=\dfrac{\sqrt{3\;}}{2} \),
\( \sin 30°=\dfrac{1}{2} \),
\( \cos 60°=\dfrac{1}{2} \), \( \operatorname{sen}60°\dfrac{\sqrt{3\;}}{2} \).
\( \cos 60°=\dfrac{1}{2} \), \( \operatorname{sen}60°\dfrac{\sqrt{3\;}}{2} \).
\[
\left\{
\begin{array}{l}
\dfrac{1}{2}T_A-\dfrac{\sqrt{3\;}}{2}T_B=0 \\
\dfrac{\sqrt{3\;}}{2}T_A-\dfrac{1}{2}T_B-100=0
\end{array}
\right.
\]
Este es un sistema de dos ecuaciones con dos incógnitas (TA y TB).
Aislando el valor de TA en la primera ecuación del sistema y sustituyendo en la segunda
ecuación
\[
\begin{gather}
\frac{1}{\cancel 2}T_A=\frac{\sqrt{3\;}}{\cancel 2}T_B\\[5pt]
T_A=\sqrt{3\;}\;T_B \tag{VI}
\end{gather}
\]
\[
\begin{gather}
\frac{\sqrt{3\;}}{2}\times\sqrt{3\;}\;T_B-\frac{1}{2}T_B-100=0 \\[5pt]
\frac{3}{2}T_B-\frac{1}{2}T_B=100 \\[5pt]
\frac{2}{2}T_B=100
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_B=100\;\mathrm N}
\end{gather}
\]
sustituyendo el valor encontrado anteriormente en la ecuación (VI), obtenemos TA
\[
\begin{gather}
T_A=\sqrt{3\;}\times 100
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_A \approx 173\;\mathrm N}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .