Exercice Résolu sur les Mouvement Relatif
publicité   



Un ouvrier tient une des extrémités d'une planche droite, de longueur a, tandis que l'autre extrémité repose sur un tambour cylindrique de manière à ce que la planche soit en position horizontale. En déplaçant la planche vers l'avant, l'ouvrier fait rouler le tambour, sans glisser le long du plan horizontal, et pendant le déplacement, la planche reste horizontale. Déterminer la distance d que l'ouvrier parcourra jusqu'à ce que l'extrémité qu'il tient touche le tambour.


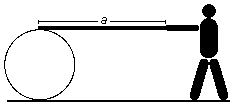
Données du problème:
  • Longueur de la planche:    a.
Solution

Appelons X la vitesse du centre du tambour par rapport au sol, X la vitesse du point de contact entre le tambour et la planche par rapport au centre du tambour et X la vitesse du point de contact entre le tambour et la planche par rapport au sol (Figure 1). La vitesse du centre du tambour sera v, la vitesse du point de contact par rapport au centre sera également v (si cette vitesse était plus grande ou plus petite, le tambour se déformerait), donc nous pouvons calculer la vitesse du point de contact par rapport au sol.
Figure 1

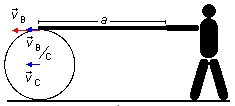
\[ \begin{gather} {\vec v}_{\small B}={\vec v}_{\small C}+{\vec v}_{\small{B/C}} \end{gather} \]
comme tous les vecteurs ont la même direction, en module
\[ \begin{gather} v_{\small B}=v+v\\[5pt] v_{\small B}=2v \end{gather} \]
Figure 2

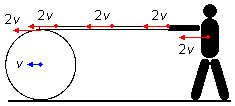
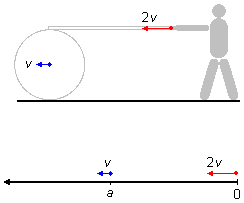
Comme la planche passe à travers le tambour sans glisser, tous les points de la planche ont la même vitesse 2v que le point de contact. Le point de contact de l'ouvrier avec la planche a également une vitesse de 2v, l'ouvrier lui-même se déplace avec une vitesse de 2v (Figure 2).

Figure 3

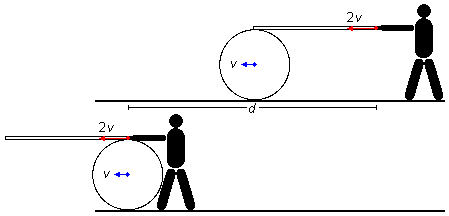
Le problème commence avec une extrémité de la planche tenue par l'ouvrier et l'autre extrémité appuyée sur le tambour, ce point d'appui est exactement sur le centre du tambour (Figure 3). Le problème se termine lorsque la main de l'ouvrier est en contact avec le tambour, à ce moment-là, elle sera sur le centre du tambour.

Alors, nous pouvons "oublier" l'ouvrier, le tambour et la planche (Figure 4) et réduire le problème à la rencontre de deux points matériels. Nous choisissons un référentiel orienté vers la gauche (contrairement à ce qui est habituellement fait), un point représentant la main de l'ouvrier partant de l'origine S0H = 0 avec une vitesse initiale v0H = vH = 2v et un autre point représentant le centre du tambour qui part d'un point S0C = a avec une vitesse v0C = vC = v. Comme les vitesses des points sont constantes, ils sont en Mouvement Rectiligne Uniforme, l'équation de ce mouvement est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_{0}+vt} \end{gather} \]
Figure 4

en écrivant cette equation pour les deux points
\[ \begin{gather} S_{\small H}=S_{0\small H}+v_{\small H}t\\[5pt] S_{\small H}=0+2vt\\[5pt] S_{\small H}=2vt \tag{I} \end{gather} \]
\[ \begin{gather} S_{\small C}=S_{0\small C}+v_{\small C}t\\[5pt] S_{\small C}=a+vt \tag{II} \end{gather} \]
pour qu'ils se rencontrent, ils doivent occuper la même position, donc nous devons imposer la condition
\[ \begin{gather} S_{\small H}=S_{\small C} \end{gather} \]
en égalant les équations (I) et (II), nous obtenons le temps nécessaire pour que les points se rencontrent
\[ \begin{gather} 2vt=a+vt\\[5pt] 2vt-vt=a\\[5pt] a=vt\\[5pt] t=\frac{a}{v} \tag{III} \end{gather} \]
en substituant l'expression (III) dans l'équation (I), nous obtenons la distance parcourue par l'homme
\[ \begin{gather} S_{\small H}=2\cancel v \frac{a}{\cancel v} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {S_{\small H}=2a} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .