Ejercicio Resuelto sobre Movimiento Relativo
publicidad
Un obrero sostiene uno de los extremos de un tablón recto, de longitud a, mientras que el otro
extremo se apoya sobre un tambor cilíndrico de manera que el tablón quede en posición horizontal. Al
mover el tablón hacia adelante, el obrero hace rodar el tambor, sin deslizarse a lo largo del plano
horizontal y durante el desplazamiento el tablón permanece horizontal. Determine la distancia d
que recorrerá el obrero hasta que el extremo sostenido por él toque el tambor.

Dado del problema:
- Longitud de la tabla: a.
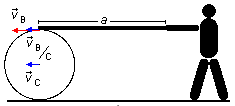
Llamemos
\( {\vec v}_{\small C} \)
a la velocidad del centro del tambor respecto al suelo,
\( {\vec v}_{\small{B/C}} \)
a la velocidad del punto de contacto entre el tambor y la tabla respecto al centro del tambor, y
\( {\vec v}_{\small B} \)
a la velocidad del punto de contacto entre el tambor y la tabla respecto al suelo (Figura 1). Tomamos
v para la velocidad del centro del tambor, la velocidad del punto de contacto respecto al centro
también será v (si esta velocidad fuera mayor o menor, el tambor se deformaría), entonces podemos
calcular la velocidad del punto de contacto respecto al suelo.
\[
\begin{gather}
{\vec v}_{\small B}={\vec v}_{\small C}+{\vec v}_{\small{B/C}}
\end{gather}
\]
dado que todos los vectores tienen la misma dirección, en módulo
\[
\begin{gather}
v_{\small B}=v+v\\[5pt]
v_{\small B}=2v
\end{gather}
\]
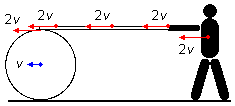
Como la tabla pasa a través del tambor sin deslizarse, todos los puntos de la tabla tienen la misma velocidad 2v que el punto de contacto. El punto de contacto del obrero con la tabla también tiene la velocidad de 2v, el propio obrero se mueve con una velocidad de 2v (Figura 2).
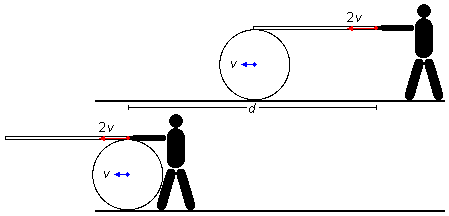
El problema comienza con un extremo de la tabla siendo sostenido por el obrero y el otro extremo apoyado en el tambor, este punto de apoyo está exactamente sobre el centro del tambor (Figura 3). El problema termina cuando la mano del obrero está en contacto con el tambor, en este momento estará sobre el centro del tambor.
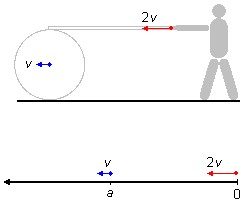
Entonces podemos "olvidar" al obrero, al tambor y a la tabla (Figura 4) y reducir el problema al
encuentro de dos partículas puntuales. Tomamos un sistema de referencia orientado hacia la izquierda
(a diferencia de lo que se hace habitualmente), un punto representa la mano del obrero partiendo desde
el origen S0HH = 0 con velocidad inicial
v0H = vH = 2v y otro punto representa el centro del
tambor que parte desde un punto S0C = a con velocidad
v0C = vC = v. Como las velocidades de los puntos son
constantes, están en Movimiento Rectilíneo Uniforme (MRU), la ecuación de este movimiento
es dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_{0}+vt}
\end{gather}
\]
escribiendo esta ecuación para los dos puntos
\[
\begin{gather}
S_{\small H}=S_{0\small H}+v_{\small H}t\\[5pt]
S_{\small H}=0+2vt\\[5pt]
S_{\small H}=2vt \tag{I}
\end{gather}
\]
\[
\begin{gather}
S_{\small C}=S_{0\small C}+v_{\small C}t\\[5pt]
S_{\small C}=a+vt \tag{II}
\end{gather}
\]
para que se encuentren, deben ocupar la misma posición, entonces debemos imponer la condición
\[
\begin{gather}
S_{\small H}=S_{\small C}
\end{gather}
\]
igualando las ecuaciones (I) y (II) obtenemos el tiempo que lleva para que los puntos se encuentren
\[
\begin{gather}
2vt=a+vt\\[5pt]
2vt-vt=a\\[5pt]
a=vt\\[5pt]
t=\frac{a}{v} \tag{III}
\end{gather}
\]
sustituyendo la expresión (III) en la ecuación (I) obtenemos la distancia recorrida por el hombre
\[
\begin{gather}
S_{\small H}=2\cancel v \frac{a}{\cancel v}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_{\small H}=2a}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .