Exercice Résolu sur les Mouvement Bidimensionnel
publicité
Du sommet d'un angle droit partent, avec un intervalle de temps égal à n secondes, deux conducteurs qui se déplacent à des vitesses constantes sur les deux côtés. Calculer les vitesses des deux conducteurs, sachant qu'après t secondes depuis le départ du deuxième conducteur, leur distance est d, et après T secondes, elle est D.
Données du problème:
- Intervalle de temps entre les départs des deux conducteurs: n;
- Distance entre les conducteurs après t secondes: d;
- Distance entre les conducteurs après T secondes: D.
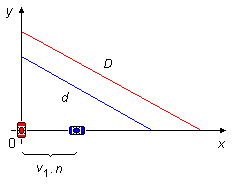
Nous choisissons un référentiel avec deux axes perpendiculaires entre eux. Le premier conducteur part de
l'origine avec une vitesse v1 dans la direction x, après n secondes le
deuxième conducteur part de l'origine avec une vitesse constante v2 dans la direction
y. Pendant l'intervalle de temps n, le conducteur 1 aura parcouru une distance égale à
v1.n, cette distance sera la position initiale du conducteur 1 au début de la
mesure du temps, le conducteur 2 qui part de l'origine aura une position initiale égale à zéro (Figure 1).
Les conducteurs ont des vitesses constantes, ils décrivent un Mouvement Rectiligne Uniforme (MRU), l'équation de ce mouvement est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v\tau} \tag{I}
\end{gather}
\]
Remarque: Ici le temps est représenté par τ au lieu de t, généralement
utilisé, pour ne pas confondre avec l'intervalle de temps t donné dans le problème.
En écrivant l'équation (I) pour les conducteurs 1 et 2 dans les intervalles de temps t et T
\[
\begin{gather}
S_1(\tau)=S_{01}+v_1\tau\\[5pt]
S_1(t)=v_1 n+v_1 t=v_1(n+t) \tag{II}\\[5pt]
S_1(T)=v_1 n+v_1 T=v_1(n+T) \tag{III}
\end{gather}
\]
\[
\begin{gather}
S_2(\tau)=S_{02}+v_2\tau\\[5pt]
S_2(t)=0+v_2t=v_2t \tag{IV}\\[5pt]
S_2(T)=0+v_2T=v_2T \tag{V}
\end{gather}
\]
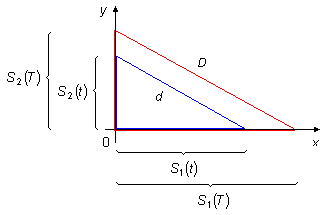
Dans la Figure 2, nous avons S1(t) le déplacement parcouru par le conducteur 1 dans
l'intervalle de temps t, et S2(t) le déplacement parcouru par le conducteur 2
dans cet intervalle de temps, en utilisant le Théorème de Pythagore
\[
\begin{gather}
h^2=S_1(t)^2+S_2(t)^2 \tag{VI}
\end{gather}
\]
En substituant les équations (II), (III), (IV) et (V) dans la condition (VI)
\[
\left\{
\begin{array}{l}
d^2=[v_1(n+t)]^2+v_2^2t^2\\
D^2=[v_1(n+T)]^2+v_2^2T^2 \tag{VII}
\end{array}
\right.
\]
c'est un système de deux équations à deux inconnues, v1 et v2, en isolant
\( v_2^2 \) dans la première équation du système (VII)
\[
\begin{gather}
v_2^2=\frac{d^2-[v_1(n+t)]^2}{t^2} \tag{VIII}
\end{gather}
\]
en substituant cette valeur dans la deuxième équation du système (VII)
\[
\begin{gather}
D^2=[v_1(n+T)]^2+\left\{\frac{d^2-[v_1(n+t)]^2}{t^2}\right\}T^2
\end{gather}
\]
\[
\begin{gather}
D^2t^2=[v_1(n+T)]^2t^2+\left\{\frac{d^2-[v_1(n+t)]^2}{\cancel{t^2}}\right\}T^2\cancel{t^2}\\[5pt]
D^2t^2=[v_1(n+T)]^2t^2+\left\{d^2-[v_1(n+t)]^2\right\}T^2\\[5pt]
D^2t^2=[v_1(n+T)]^2t^2+d^2T^2-[v_1(n+t)]^2T^2\\[5pt]
D^2t^2-d^2T^2=v_1^2(n+T)^2t^2-v_1^2(n+t)^2T^2
\end{gather}
\]
en factorisant
\( v_1^2 \)
du côté droit de l'équation
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2[(n+T)^2t^2-(n+t)^2T^2]
\end{gather}
\]
Des Identité Remarquable
\[
\begin{gather}
(a+b)^2=a^2+2ab+b^2
\end{gather}
\]
en appliquant ce produit aux termes \( (n+T)^2 \) et \( (n+t)^2 \)
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2[(n^2+2nT+T^2)t^2-(n^2+2nt+t^2)T^2]\\[5pt]
D^2t^2-d^2T^2=v_1^2[n^2t^2+2nTt^2+T^2t^2-n^2T^2-2ntT^2-t^2T^2]\\[5pt]
D^2t^2-d^2T^2=v_1^2[n^2t^2+2nTt^2-n^2T^2-2ntT^2]
\end{gather}
\]
en factorisant n2 et 2ntT dans le terme entre crochets
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2[n^2(t^2-T^2)+2ntT(t-T)]
\end{gather}
\]
Des Identité Remarquable
\[
\begin{gather}
\left(a^2-b^2\right)=(a+b)(a-b)
\end{gather}
\]
en appliquant ce produit au terme \( \left(t^2-T^2\right) \)
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2[n^2(t+T)(t-T)+2ntT(t-T)]
\end{gather}
\]
en factorisant le terme n(t-T) dans les crochets
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2\left\{n(t-T)\left[n(t+T)+2tT\right]\right\}\\[5pt]
v_1^2=\frac{D^2t^2-d^2T^2}{n(t-T)\left[n(t+T)+2tT\right]} \tag{IX}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_1=\pm\sqrt{\frac{D^2t^2-d^2T^2}{n(t-T)\left[n(t+T)+2tT\right]}}}
\end{gather}
\]
En substituant cette valeur en
\( v_1^2 \),
donné sous la forme de l'équation (IX), dans l'équation (VIII) et en factorisant le terme
\( \frac{1}{t^2} \),
nous aurons la valeur de v2
\[
\begin{gather}
v_2^2=\frac{d^2-[v_1(n+t)]^2}{t^2}\\[5pt]
v_2^2=\frac{1}{t^2}\left[d^2-v_1^2(n+t)^2\right]\\[5pt]
v_2^2=\frac{1}{t^2}\left\{d^2-\frac{D^2t^2-d^2T^2}{n(t-T)\left[n(t+T)+2tT\right]}(n+t)^2\right\}
\end{gather}
\]
le terme
\( n(t-T)\left[n(t+T)+2tT\right] \)
est le facteur commun des termes entre accolades
\[
\begin{gather}
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[n(t-T)\left[n(t+T)+2tT\right]\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[n^2(t+T)(t-T)+2tTn(t-T)\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[n^2(t^2-T^2)+2t^2Tn-2tT^2n\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[n2t^2-n^2T^2+2t^2Tn-2tT^2n\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}
\end{gather}
\]
dans le terme entre crochets
\( n^2t^2-n^2T^2+2t^2Tn-2tT^2n \),
nous allons regrouper les termes de la manière suivante
\( (n^2t^2+2t^2Tn)+(-n^2T^2-2tT^2n). \)
\[ (n^2t^2+2t^2Tn)+(-n^2T^2-2tT^2n) \]
.
Dans le premier terme entre parenthèses, nous factorisons t2 et dans le deuxième terme,
nous factorisons
\( -T^2 \)
\[
\begin{gather}
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[(n^2t^2+2t^2Tn)+(-n^2T^2-2tT^2n)\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[t^2(n^2+2Tn)-T^2(n^2+2tn)\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}
\end{gather}
\]
dans le terme entre crochets, nous allons additionner et soustraire T2 dans le premier
terme entre parenthèses et dans le deuxième terme entre parenthèses, nous allons additionner et soustraire
t2.
Remarque: Les termes entre parenthèses
\( n^2+2Tn \)
et
\( n^2+2tn \)
sont similaires à la Identité Remarquable
\( a^2+2ab+b^2=(a+b)^2 \),
sauf pour le terme b2 qui manque
(T2 dans la première équation et t2 dans la deuxième équation). Nous
pouvons donc utiliser la Méthode du Complétion du Carré, si nous avons une équation de la forme
\( a^2+2ab \)
en additionnant et en soustrayant le carré du terme manquant, rien ne change, nous ajoutons zéro dans
l'équation
\( a^2+2ab+\underbrace{b^2-b^2}_{0} \),
Les trois premiers termes forment de la Identité Remarquable
\( \underbrace{a^2+2ab+b^2}_{(a+b)^2}-b^2 \),
donc nous pouvons écrire notre équation originale sous la forme
\( a^2+2ab=(a+b)^2-b^2 \).
\[
\begin{gather}
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[(n^2+2Tn+T^2-T^2)t^2-(n^2+2tn+t^2-t^2)T^2\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}
\end{gather}
\]
les termes
\( n^2+2Tn+T^2 \)
et
\( n^2+2tn+t^2 \)
sont de la même forme que la Identité Remarquable
\( (a+b)^2 \)
\[
\begin{gather}
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[((n+T)^2-T^2)t^2-((n+t)^2-t^2)T^2\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[(n+T)^2t^2-T^2t^2-(n+t)^2T^2+t^2T^2\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[(n+T)^2t^2-(n+t)^2T^2\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[\;n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2(n+T)^2t^2-d^2(n+t)^2T^2-D^2(n+t)^2t^2+d^2(n+t)^2T^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2(n+T)^2t^2-D^2(n+t)^2t^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{d^2(n+T)^2-D^2(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_2=\pm\sqrt{\frac{d^2(n+T)^2-D^2(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}}}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .