Ejercicio Resuelto sobre Movimiento Bidimensional
publicidad
Desde el vértice de un ángulo recto parten, con un intervalo de tiempo igual a n segundos, dos conductores, que se desplazan con velocidades constantes sobre los dos lados. Calcular las velocidades de los dos conductores, sabiendo que después de t segundos, desde la salida del segundo conductor, su distancia es d, y después de T segundos es D.
Datos del problema:
- Intervalo de tiempo entre las salidas de los dos conductores: n;
- Distancia entre los móviles después de t segundos: d;
- Distancia entre los móviles después de T segundos: D.
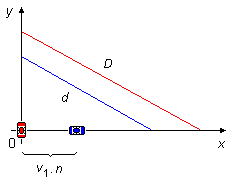
Tomamos un sistema de referencia con 2 ejes perpendiculares entre sí. El primer móvil parte del origen
con velocidad v1 en la dirección x, después de n segundos el segundo
móvil parte del origen con velocidad constante v2 en la dirección y. Durante el
intervalo de tiempo n el móvil 1 habrá recorrido una distancia igual a
v1.n, esta distancia será la posición inicial del móvil 1 cuando comience la
cuenta del tiempo, el móvil 2 que parte del origen tendrá posición inicial igual a cero (Figura 1).
Los móviles tienen velocidades constantes, describen un Movimiento Rectilíneo Uniforme (MRU), la ecuación de este movimiento está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v\tau} \tag{I}
\end{gather}
\]
Observación: Aquí el tiempo está representado por τ en lugar de t,
generalmente usado, para no confundir con el intervalo de tiempo t dado en el problema.
Escribiendo la ecuación (I) para móviles 1 y 2 en los intervalos de tiempo t y T
\[
\begin{gather}
S_1(\tau)=S_{01}+v_1\tau\\[5pt]
S_1(t)=v_1 n+v_1 t=v_1(n+t) \tag{II}\\[5pt]
S_1(T)=v_1 n+v_1 T=v_1(n+T) \tag{III}
\end{gather}
\]
\[
\begin{gather}
S_2(\tau)=S_{02}+v_2\tau\\[5pt]
S_2(t)=0+v_2t=v_2t \tag{IV}\\[5pt]
S_2(T)=0+v_2T=v_2T \tag{V}
\end{gather}
\]
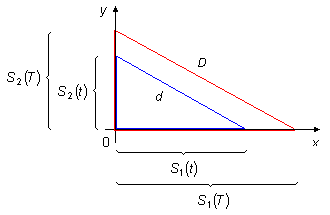
En la Figura 2 tenemos, S1(t) el espacio recorrido por el móvil 1 en el intervalo de
tiempo t, y S2(t) el espacio recorrido por el móvil 2 en este intervalo de
tiempo, usando el Teorema de Pitágoras
\[
\begin{gather}
h^2=S_1(t)^2+S_2(t)^2 \tag{VI}
\end{gather}
\]
Sustituyendo las ecuaciones (II), (III), (IV) y (V) en la condición (VI)
\[
\left\{
\begin{array}{l}
d^2=[v_1(n+t)]^2+v_2^2t^2\\
D^2=[v_1(n+T)]^2+v_2^2T^2 \tag{VII}
\end{array}
\right.
\]
este es un sistema de dos ecuaciones con dos incógnitas, v1 y v2,
aislando \( v_2^2 \) en la primera ecuación del sistema (VII)
\[
\begin{gather}
v_2^2=\frac{d^2-[v_1(n+t)]^2}{t^2} \tag{VIII}
\end{gather}
\]
sustituyendo este valor en la segunda ecuación del sistema (VII)
\[
\begin{gather}
D^2=[v_1(n+T)]^2+\left\{\frac{d^2-[v_1(n+t)]^2}{t^2}\right\}T^2
\end{gather}
\]
\[
\begin{gather}
D^2t^2=[v_1(n+T)]^2t^2+\left\{\frac{d^2-[v_1(n+t)]^2}{\cancel{t^2}}\right\}T^2\cancel{t^2}\\[5pt]
D^2t^2=[v_1(n+T)]^2t^2+\left\{d^2-[v_1(n+t)]^2\right\}T^2\\[5pt]
D^2t^2=[v_1(n+T)]^2t^2+d^2T^2-[v_1(n+t)]^2T^2\\[5pt]
D^2t^2-d^2T^2=v_1^2(n+T)^2t^2-v_1^2(n+t)^2T^2
\end{gather}
\]
factorizando
\( v_1^2 \)
en el lado derecho de la ecuación
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2[(n+T)^2t^2-(n+t)^2T^2]
\end{gather}
\]
De los Productos Notables
\[
\begin{gather}
(a+b)^2=a^2+2ab+b^2
\end{gather}
\]
aplicando este producto a los términos \( (n+T)^2 \) y \( (n+t)^2 \)
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2[(n^2+2nT+T^2)t^2-(n^2+2nt+t^2)T^2]\\[5pt]
D^2t^2-d^2T^2=v_1^2[n^2t^2+2nTt^2+T^2t^2-n^2T^2-2ntT^2-t^2T^2]\\[5pt]
D^2t^2-d^2T^2=v_1^2[n^2t^2+2nTt^2-n^2T^2-2ntT^2]
\end{gather}
\]
factorizando n2 y 2ntT en el término entre corchetes
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2[n^2(t^2-T^2)+2ntT(t-T)]
\end{gather}
\]
De los Productos Notables
\[
\begin{gather}
\left(a^2-b^2\right)=(a+b)(a-b)
\end{gather}
\]
aplicando este producto al término \( \left(t^2-T^2\right) \)
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2[n^2(t+T)(t-T)+2ntT(t-T)]
\end{gather}
\]
factorizando el término n(t-T) en evidencia dentro de los corchetes
\[
\begin{gather}
D^2t^2-d^2T^2=v_1^2\left\{n(t-T)\left[n(t+T)+2tT\right]\right\}\\[5pt]
v_1^2=\frac{D^2t^2-d^2T^2}{n(t-T)\left[n(t+T)+2tT\right]} \tag{IX}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_1=\pm\sqrt{\frac{D^2t^2-d^2T^2}{n(t-T)\left[n(t+T)+2tT\right]}}}
\end{gather}
\]
Sustituyendo este valor en
\( v_1^2 \),
dado en la forma de la ecuación (IX), en la ecuación (VIII) y factorizando el término
\( \frac{1}{t^2} \)
tendremos el valor de v2
\[
\begin{gather}
v_2^2=\frac{d^2-[v_1(n+t)]^2}{t^2}\\[5pt]
v_2^2=\frac{1}{t^2}\left[d^2-v_1^2(n+t)^2\right]\\[5pt]
v_2^2=\frac{1}{t^2}\left\{d^2-\frac{D^2t^2-d^2T^2}{n(t-T)\left[n(t+T)+2tT\right]}(n+t)^2\right\}
\end{gather}
\]
el término
\( n(t-T)\left[n(t+T)+2tT\right] \)
es el factor común de los términos entre llaves
\[
\begin{gather}
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[n(t-T)\left[n(t+T)+2tT\right]\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[n^2(t+T)(t-T)+2tTn(t-T)\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[n^2(t^2-T^2)+2t^2Tn-2tT^2n\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[n2t^2-n^2T^2+2t^2Tn-2tT^2n\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}
\end{gather}
\]
en el término entre corchetes
\( n^2t^2-n^2T^2+2t^2Tn-2tT^2n \),
agruparemos los términos de la siguiente manera
\( (n^2t^2+2t^2Tn)+(-n^2T^2-2tT^2n). \)
\[ (n^2t^2+2t^2Tn)+(-n^2T^2-2tT^2n) \]
.
En el primer término entre paréntesis factorizamos t2 y en el segundo término factorizamos
\( -T^2 \)
\[
\begin{gather}
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[(n^2t^2+2t^2Tn)+(-n^2T^2-2tT^2n)\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[t^2(n^2+2Tn)-T^2(n^2+2tn)\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}
\end{gather}
\]
en el término entre corchetes sumaremos y restaremos T2 en el primer término entre
paréntesis y en el segundo término entre paréntesis sumaremos y restaremos t2.
Observación: Los términos entre paréntesis
\( n^2+2Tn \)
y
\( n^2+2tn \)
son semejantes al Producto Notable
\( a^2+2ab+b^2=(a+b)^2 \),
a menos del término b2 que falta
(T2 en la primera ecuación y t2 en la segunda ecuación).
Entonces podemos usar el Método de Completar Cuadrados, si tenemos una ecuación de la forma \( a^2+2ab \) sumando y restando el cuadrado del término que falta nada se altera, estamos sumando cero en la ecuación, \( a^2+2ab+\underbrace{b^2-b^2}_{0} \), Los tres primeros términos forman un Producto Notable \( \underbrace{a^2+2ab+b^2}_{(a+b)^2}-b^2 \), entonces podemos escribir nuestra ecuación original en la forma \( a^2+2ab=(a+b)^2-b^2 \).
Entonces podemos usar el Método de Completar Cuadrados, si tenemos una ecuación de la forma \( a^2+2ab \) sumando y restando el cuadrado del término que falta nada se altera, estamos sumando cero en la ecuación, \( a^2+2ab+\underbrace{b^2-b^2}_{0} \), Los tres primeros términos forman un Producto Notable \( \underbrace{a^2+2ab+b^2}_{(a+b)^2}-b^2 \), entonces podemos escribir nuestra ecuación original en la forma \( a^2+2ab=(a+b)^2-b^2 \).
\[
\begin{gather}
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[(n^2+2Tn+T^2-T^2)t^2-(n^2+2tn+t^2-t^2)T^2\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}
\end{gather}
\]
los términos
\( n^2+2Tn+T^2 \)
y
\( n^2+2tn+t^2 \)
son de la misma forma del Producto Notable
\( (a+b)^2 \)
\[
\begin{gather}
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[((n+T)^2-T^2)t^2-((n+t)^2-t^2)T^2\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[(n+T)^2t^2-T^2t^2-(n+t)^2T^2+t^2T^2\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2\left[(n+T)^2t^2-(n+t)^2T^2\right]-(D^2t^2-d^2T^2)(n+t)^2}{n(t-T)\left[\;n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2(n+T)^2t^2-d^2(n+t)^2T^2-D^2(n+t)^2t^2+d^2(n+t)^2T^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{1}{t^2}\left\{\frac{d^2(n+T)^2t^2-D^2(n+t)^2t^2}{n(t-T)\left[n(t+T)+2tT\right]}\right\}\\[5pt]
v_2^2=\frac{d^2(n+T)^2-D^2(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_2=\pm\sqrt{\frac{d^2(n+T)^2-D^2(n+t)^2}{n(t-T)\left[n(t+T)+2tT\right]}}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .