Exercice Résolu sur les Mouvement Bidimensionnel
publicité
De deux points A et B situés à une distance de 1000 m l'un de l'autre, sur un même plan
horizontal, deux fusées sont lancées simultanément. L'une part du point B avec une vitesse
initiale de 200 m/s dirigée de bas en haut et l'autre part du point A en direction de la verticale
qui passe par B, formant un angle de 60° avec l'horizon. Déterminer:
a) La vitesse initiale de la fusée A pour intercepter la seconde;
b) Après combien de temps se fait la rencontre des deux fusées;
c) À quelle hauteur se fait la rencontre;
d) Vérifier si cette rencontre se fait pendant la montée ou la descente de la première fusée.
a) La vitesse initiale de la fusée A pour intercepter la seconde;
b) Après combien de temps se fait la rencontre des deux fusées;
c) À quelle hauteur se fait la rencontre;
d) Vérifier si cette rencontre se fait pendant la montée ou la descente de la première fusée.
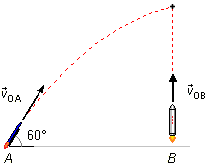
Données du problème:
- Distance entre les points A et B de lancement: d = 1000 m;
- Angle de lancement de la fusée A: θ = 60°;
- Vitesse initiale de la fusée B: v0B = 200 m/s;
- Accélération de la pesanteur: g = 9,8 m/s2.
Nous choisissons un référentiel au sol avec l'axe Ox pointant vers la droite et Oy vers le haut, l'accélération de la pesanteur pointant vers le bas et le point de départ de la fusée A étant en (x0A, y0A) = (0, 0), et la fusée B étant en (x0B, y0B) = (0, 1000), (Figure 1).
Solution
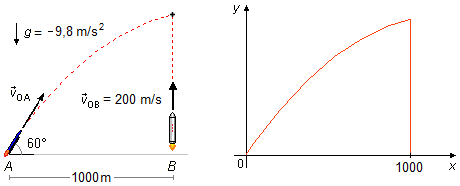
Le mouvement de la fusée lancée de A peut être décomposé sur les axes x et y. La
vitesse initiale v0A avec laquelle elle est lancée a des composantes dans les
directions x et y (Figure 2).
\[
\begin{gather}
v_{0Ax}=v_{0A}\cos 60°\\[10pt]
v_{0Ay}=v_{0A}\operatorname{sen}60°
\end{gather}
\]
D'après la Trigonométrie,
\( \cos 60°=\dfrac{1}{2} \)
et
\( \operatorname{sen}60°=\dfrac{\sqrt{3\;}}{2} \)
\[
\begin{gather}
v_{0Ax}=\frac{1}{2}v_{0A} \tag{I}
\end{gather}
\]
\[
\begin{gather}
v_{0Ay}=\frac{\sqrt{3\;}}{2}v_{0A} \tag{II}
\end{gather}
\]
Dans la direction x, il n'y a pas d'accélération agissant sur la fusée, elle est en
Mouvement Uniforme (MU) et son mouvement est donné par l'équation
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt}
\end{gather}
\]
comme dans le mouvement uniforme vAx = v0Ax est constant, nous
pouvons remplacer vAx par la valeur de (I) et S0Ax = 0
\[
\begin{gather}
S_{Ax}=S_{0Ax}+v_{Ax}t\\[5pt]
S_{Ax}=0+\frac{1}{2}v_{0A}t\\[5pt]
S_{Ax}=\frac{1}{2}v_{0A}t \tag{III}
\end{gather}
\]
Dans la direction y, la fusée est sous l'action de l'accélération de la pesanteur, elle est en
Mouvement Uniformément Varié (MUV), les équations de la position et de la vitesse sont
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0 t-\frac{g}{2}t^2} \tag{IV}
\end{gather}
\]
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=v_0-gt}
\end{gather}
\]
en remplaçant v0Ay par la valeur donnée en (II) et S0Ay = 0
\[
\begin{gather}
S_{Ay}=S_{0Ay}+v_{0Ay}t-\frac{g}{2}t^2\\[5pt]
S_{Ay}=0+\frac{\sqrt{3\;}}{2}v_{0A}t-\frac{9,8}{2}t^2\\[5pt]
S_{Ay}=\frac{\sqrt{3\;}}{2}v_{0A}t-4,9t^2 \tag{V}
\end{gather}
\]
\[
\begin{gather}
v_{Ay}=v_{0ay}-gt\\[5pt]
v_{Ay}=\frac{\sqrt{3\;}}{2}v_{0A}-9,8t \tag{VI}
\end{gather}
\]
le signe négatif indique que l'accélération de la pesanteur est opposée à l'orientation du référentiel.
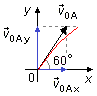
Dans la Figure 3, nous voyons que dans le mouvement le long de la direction x, nous avons pour des
intervalles de temps égaux des intervalles de déplacement égaux
(Δx1 = Δx2 =
Δx3 = Δx4 = Δx5 =
Δx6).
Dans la direction y, au moment où la fusée est lancée, la vitesse vy commence à
diminuer; pour des intervalles de temps égaux, nous avons des intervalles de déplacement de plus en plus
petits
(Δy1 > Δy2 > Δy3 >
Δy4 > Δy5 > Δy6).
La fusée lancée de B n'a qu'un mouvement le long de l'axe y, elle est sous l'action de l'accélération de la pesanteur en Mouvement Uniformément Varié (MUV), en appliquant l'équation (IV)
La fusée lancée de B n'a qu'un mouvement le long de l'axe y, elle est sous l'action de l'accélération de la pesanteur en Mouvement Uniformément Varié (MUV), en appliquant l'équation (IV)
\[
\begin{gather}
S_B=S_{0B}+v_{0B}t-\frac{g}{2}t^2
\end{gather}
\]
en remplaçant v0B par la valeur donnée dans le problème et S0B = 0
\[
\begin{gather}
S_B=0+200t-\frac{9,8}{2}t^2\\[5pt]
S_B=200t-4,9t^2 \tag{VII}
\end{gather}
\]
a) Pour que la rencontre ait lieu, nous devons avoir la condition
\[
\begin{gather}
S_{Ay}=S_B
\end{gather}
\]
\[
\begin{gather}
\frac{\sqrt{3\;}}{2}v_{0A}t-4,9t^2=200t-4,9t^2\\[5pt]
\frac{\sqrt{3\;}}{2}v_{0A}t=200t-4,9t^2+4,9t^2\\[5pt]
\frac{\sqrt{3\;}}{2}v_{0A}\cancel t=200\cancel t\\[5pt]
v_{0A}=\frac{2\times 200}{\sqrt{3\;}}\\[5pt]
v_{0A}=\frac{400}{\sqrt{3\;}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_{0A}\approx 231\;\mathrm{m/s}}
\end{gather}
\]
b) Comme la fusée partant de B monte verticalement, la fusée partant de A doit parcourir la distance de 1000 m dans la direction x pour l'intercepter, en remplaçant la valeur de l'item précédent et SAx = 1000 m dans l'équation (III)
\[
\begin{gather}
1000=\frac{1}{2}\times 231t\\[5pt]
t=\frac{2\times 1000}{231}\\[5pt]
t=\frac{2000}{231}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t\approx 8,6\;\mathrm{s}}
\end{gather}
\]
c) La fusée B montera verticalement jusqu'à ce que la rencontre ait lieu, en remplaçant la valeur de l'item précédent dans l'équation (VII)
\[
\begin{gather}
S_B=200\times 8,6-4,9\times 8,6^2\\[5pt]
S_B=1720-362
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_B\approx 1358\;\mathrm m}
\end{gather}
\]
Remarque: Nous pourrions trouver la même valeur en remplaçant la vitesse de l'item (a) et
l'intervalle de temps trouvé en (b) dans l'équation (V).
d) Si l'instant de la rencontre est inférieur à l'intervalle de temps pour que la fusée A atteigne la hauteur maximale, la rencontre se fera pendant la montée; si l'instant est supérieur, la rencontre se fera pendant la descente. Lorsque la fusée partant de A atteint la hauteur maximale, la composante de sa vitesse dans la direction y s'annule vAy = 0, le temps que la fusée de A met pour atteindre cette hauteur sera obtenu en remplaçant cette condition et la vitesse de l'item (a) dans l'équation (VI)
\[
\begin{gather}
0=\frac{\sqrt{3\;}}{2}\times 231-9,8t\\[5pt]
\frac{\sqrt{3\;}}{2}\times 231=9,8t\\[5pt]
t=\frac{\sqrt{3\;}\times 231}{2\times 9,8}\\[5pt]
t\approx 20,4\;\mathrm s
\end{gather}
\]
Comme l'intervalle de temps pour que la fusée atteigne la hauteur maximale est supérieur à l'intervalle de
temps pour que la rencontre ait lieu, la rencontre se fait pendant la
montée de la première fusée.
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .