Exercice Résolu sur les Condensateurs

On utilise 12 condensateurs de valeur C égale pour construire les arêtes d'un cube comme indiqué dans la figure. Calculer le condensateur équivalent entre les points A et G qui forment l'une des diagonales principales du cube.

Solution

Nous supposons que les condensateurs sont déjà chargés, en négligeant le transitoire pendant le temps de charge des condensateurs.

Le point A est un nœud du circuit, la différence de potentiel entre les points A et B, A et D, A et E est la même, donc les points B, D et E représentent un même point du circuit, \( B\equiv D\equiv E \). Les trois condensateurs "partent" du point commun A et "arrivent" au point commun \( B\equiv D\equiv E \), donc ces trois condensateurs sont en parallèle (Figure 1).

Figure 1

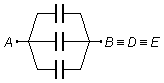
Les trois condensateurs placés entre les points

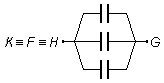
K et G, F et G, H et G sont également soumis à la même différence de potentiel, les points K, F et H représentent donc un même point du circuit, \( K\equiv F\equiv H \). Les condensateurs "partent" du point commun \( K\equiv F\equiv H \) et "arrivent" au point commun G. ceux-ci sont également en parallèle (Figure 2).

Figure 2

Les autres condensateurs sont tous placés entre les points communs \( B\equiv D\equiv E \) et \( K\equiv F\equiv H \), ils sont tous en parallèle (Figure 3).

Figure 3

Le circuit en cube est équivalent à un circuit plan formé par trois condensateurs en parallèle, en série avec six condensateurs en parallèle et en série avec trois autres condensateurs en parallèle (Figure 4).

Figure 4

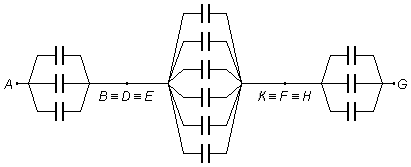
En appelant C₁ le condensateur équivalent entre les points A et \( B\equiv D\equiv E \) et C₃ le condensateur équivalent entre les points \( K\equiv F\equiv H \) et G, comme ces parties du circuit sont identiques, nous avons C₁ = C₃. L'expression pour déterminer le condensateur équivalent d'une association de n condensateurs égaux connectés en parallèle est

\[ \begin{gather} \bbox[#99CCFF,10px] {C_{eq}=nC} \end{gather} \]

pour n = 3

\[ \begin{gather} C_1=C_3=3C \end{gather} \]

Remarque: nous pourrions également déterminer le condensateur équivalent en appliquant l'expression générale pour l'association de condensateurs en parallèle

\[ \begin{gather} C_{eq}=\sum_{i=1}^{n}C_{i}\\[5pt] C_1=C_3=C+C+C\\[5pt] C_1=C_3=3C \end{gather} \]

Entre les points \( B\equiv D\equiv E \) et \( K\equiv F\equiv H \), nous avons six condensateurs égaux en parallèle, en appelant le condensateur équivalent entre ces points C₂, en appliquant à nouveau l'expression pour l'association en parallèle de condensateurs de valeur égale avec n = 6.

\[ \begin{gather} C_2=6C \end{gather} \]

Remarque: ou en appliquant l'expression générale pour l'association de condensateurs en parallèle

\[ \begin{gather} C_2=C+C+C+C+C+C\\[5pt] C_2=6C \end{gather} \]

Ainsi, le circuit se réduit comme suit

Figure 5

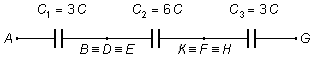
Le condensateur équivalent du circuit C_eq sera la somme des condensateurs en série

\[ \begin{gather} \bbox[#99CCFF,10px] {\frac{1}{C_{eq}}=\sum _{i=1}^{n}{\frac{1}{C_i}}} \end{gather} \]

\[ \begin{gather} \frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\\[5pt] \frac{1}{C_{eq}}=\frac{1}{3C}+\frac{1}{6C}+\frac{1}{3C} \end{gather} \]

le facteur commun entre 3C et 6C est 6C

\[ \begin{gather} \frac{1}{C_{eq}}=\frac{2+1+2}{6C}\\[5pt] \frac{1}{C_{eq}}=\frac{5}{6C} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {C_{eq}=\frac{6C}{5}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .