Ejercicio Resuelto sobre Condensadores
publicidad   



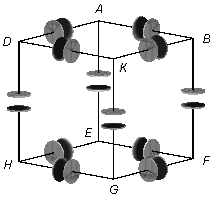
Se utilizan 12 condensadores iguales de valor C para construir las aristas de un cubo como se indica en la figura. Calcular el capacitor equivalente entre los puntos A y G que forman una de las diagonales principales del cubo.


Solution

Consideremos que los condensadores ya están cargados, despreciando el transitorio durante el tiempo de carga de los condensadores.
El punto A es un nodo del circuito y la caída de tensión entre los puntos A y B, A y D, A y E es la misma, por lo tanto, los puntos B, D y E representan un mismo punto del circuito, \( B\equiv D\equiv E \). Los tres condensadores "salen" del punto en común A y "llegan" al punto en común \( B\equiv D\equiv E \), por lo tanto, estos tres condensadores están en paralelo (Figura 1).
Figura 1

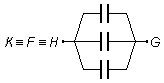
Los tres capacitores colocados entre los puntos K y G, F y G, H y G también están bajo la misma diferencia de potencial, los puntos K, F y H representan, entonces, un mismo punto del circuito, \( K\equiv F\equiv H \). Los capacitores "salen" del punto común \( K\equiv F\equiv H \) y "llegan" al punto común G. Estos también están en paralelo (Figura 2).
Figura 2

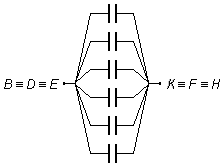
Los demás capacitores están todos colocados entre los puntos comunes \( B\equiv D\equiv E \) y \( K\equiv F\equiv H \), todos están en paralelo (Figura 3).

Figura 3

El circuito en forma de cubo es equivalente a un circuito plano formado por tres capacitores en paralelo, en serie con seis capacitores en paralelo y en serie con otros tres capacitores en paralelo (Figura 4).

Figura 4

Llamaremos C1 al capacitor equivalente entre los puntos A y \( B\equiv D\equiv E \) y C3 al capacitor equivalente entre los puntos \( K\equiv F\equiv H \) y G. Como estas partes del circuito son iguales, tenemos que C1 = C3. La expresión para determinar el capacitor equivalente de una asociación de n capacitores iguales conectados en paralelo es
\[ \begin{gather} \bbox[#99CCFF,10px] {C_{eq}=nC} \end{gather} \]
para n = 3
\[ \begin{gather} C_1=C_3=3C \end{gather} \]
Observación: también podríamos determinar el capacitor equivalente aplicando la expresión general para la asociación de capacitores en paralelo
\[ \begin{gather} C_{eq}=\sum_{i=1}^{n}C_{i}\\[5pt] C_1=C_3=C+C+C\\[5pt] C_1=C_3=3C \end{gather} \]

Entre los puntos \( B\equiv D\equiv E \) y \( K\equiv F\equiv H \) tenemos seis capacitores iguales en paralelo, llamaremos al capacitor equivalente entre estos puntos C2, aplicando nuevamente la expresión para la asociación en paralelo de capacitores de igual valor con n = 6
\[ \begin{gather} C_2=6C \end{gather} \]
Observación: o aplicando la expresión general para la asociación de capacitores en paralelo
\[ \begin{gather} C_2=C+C+C+C+C+C\\[5pt] C_2=6C \end{gather} \]

Así, el circuito se reduce al siguiente

Figura 5

El capacitor equivalente del circuito Ceq será la suma de los capacitores en serie
\[ \begin{gather} \bbox[#99CCFF,10px] {\frac{1}{C_{eq}}=\sum _{i=1}^{n}{\frac{1}{C_i}}} \end{gather} \]
\[ \begin{gather} \frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\\[5pt] \frac{1}{C_{eq}}=\frac{1}{3C}+\frac{1}{6C}+\frac{1}{3C} \end{gather} \]
el factor común entre 3Cye 6C es 6C
\[ \begin{gather} \frac{1}{C_{eq}}=\frac{2+1+2}{6C}\\[5pt] \frac{1}{C_{eq}}=\frac{5}{6C} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {C_{eq}=\frac{6C}{5}} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .