Exercice Résolu sur les Calorimétrie
publicité   



De quelle hauteur une certaine masse d'eau devrait-elle tomber pour que son énergie finale, convertie en chaleur, augmente la température de cette masse de 1 °C? Supposons qu'il n'y ait aucune perte.
Données: 1 cal = 4,18 J, g = 9,8 m/s2, c = 1 cal/g°C.


Données du problème:
  • Variation de la température de l'eau:    Δ t = 1 °C;
  • Chaleur massique de l'eau:    c = 1 cal/g°C;
  • Équivalent mécanique de la chaleur:    1 cal = 4,18 J;
  • Accélération de la pesanteur:    g = 9,8 m/s2.
Schéma du problème:

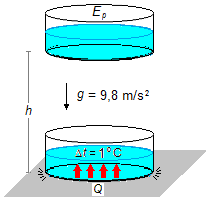
À la position initiale, à une hauteur h, toute l'énergie mécanique de la masse d'eau est sous forme d'énergie potentielle EP. Lorsque la masse atteint le sol, en supposant qu'il n'y ait aucune perte d'énergie, toute l'énergie potentielle est convertie en chaleur Q, ce qui réchauffe l'eau (Figure 1).
Figure 1
Solution:

Premièrement, nous devons convertir la chaleur spécifique de l'eau, donnée en calories par gramme-degré Celsius (cal/g°C), en joules par kilogramme-degré Celsius (J/kg°C), unité utilisée dans le Système International d'Unités (SI)
\[ \begin{gather} c=1\;\mathrm{\frac{\cancel{cal}}{\cancel g °C}}\times\frac{4,18\;\mathrm J}{1\;\mathrm{\cancel{cal}}}\times\frac{1000\;\mathrm{\cancel g}}{1\;\mathrm{kg}}=4180\;\mathrm{\frac{J}{kg°C}} \end{gather} \]
L'énergie potentielle est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {E_p=mgh} \tag{I} \end{gather} \]
La quantité de chaleur reçue par le corps est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {Q=mc\Delta t} \tag{II} \end{gather} \]
L'énergie potentielle initiale est convertie en chaleur à la fin, en égalant les équations (I) et (II)
\[ \begin{gather} E_p=Q \\[5pt] \cancel m gh=\cancel m c\Delta t \\[5pt] h=\frac{c \Delta t}{g} \end{gather} \]
en substituant les données du problème
\[ \begin{gather} h=\frac{4180\times 1}{9,8} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {h=426,5\;\mathrm m} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .