Solved Problem on Heat
advertisement
From what height should a mass of water fall so that its final energy, converted into heat, increases the temperature of this mass by 1 °C? Assume that there is no energy loss in the system.
Data: 1 cal = 4.18 J, g = 9.8 m/s2, c = 1 cal/g°C.
Problem data:
- Chabge in water temperature: Δ t = 1 °C;
- Specific heat of water: c = 1 cal/g°C;
- Mechanical equivalent of heat: 1 cal = 4.18 J;
- Acceleration due to gravity: g = 9.8 m/s2.
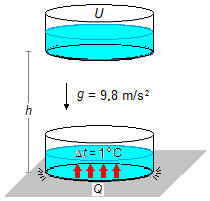
In the initial position, at the height of h, all the mechanical energy of the water mass is in
the form of potential energy U. When the mass reaches the ground, assuming that there is
no energy loss, all potential energy becomes heat Q that heats the water (Figure 1).
First, we must convert the specific heat from the water given in calories per gram-degree Celsius (cal/g °C) to joules per kilogram-degree Celsius (J/kg °C) used in the International System of Units (SI)
\[
\begin{gather}
c=1\;\mathrm{\frac{\cancel{cal}}{\cancel g °C}}\times\frac{4.18\;\mathrm J}{1\;\mathrm{\cancel{cal}}}\times\frac{1000\;\mathrm{\cancel g}}{1\;\mathrm{kg}}=4180\;\mathrm{\frac{J}{kg°C}}
\end{gather}
\]
The Potential Energy is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{U=mgh} \tag{I}
\end{gather}
\]
The equation of heat received by the body is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{Q=mc\Delta t} \tag{II}
\end{gather}
\]
The initial potential energy is converted into heat at the end, equating equations (I) and (II)
\[
\begin{gather}
U=Q \\[5pt]
\cancel m gh=\cancel m c\Delta t \\[5pt]
h=\frac{c \Delta t}{g}
\end{gather}
\]
substituting the problem data
\[
\begin{gather}
h=\frac{\left(4180\;\mathrm{\frac{J}{kg\cancel{°C}}}\right)(1\;\mathrm{\cancel{°C}})}{9.8\;\mathrm{\frac{m}{s^2}}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{h=426.5\;\text{m}}
\]
Note: in the expression of the units of h, we have
\( \displaystyle \mathrm{ \frac{\frac{J}{kg}}{\frac{m}{s²}}=J\frac{s²}{kg.m} } \)
The unit joule (J) is given by \( \displaystyle \mathrm J=\mathrm{ kg\frac{m}{s²}m } \), substituting this value of J in the expression for h \( \displaystyle \mathrm{ \cancel{kg}\frac{\cancel m}{\cancel{s²}}m\frac{\cancel{s²}}{kg.\cancel m}=m } \)
The unit of h will be the meter m
The unit joule (J) is given by \( \displaystyle \mathrm J=\mathrm{ kg\frac{m}{s²}m } \), substituting this value of J in the expression for h \( \displaystyle \mathrm{ \cancel{kg}\frac{\cancel m}{\cancel{s²}}m\frac{\cancel{s²}}{kg.\cancel m}=m } \)
The unit of h will be the meter m
\[
[h]=m
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .